When you see X ⊃ Y, you are to read "X implies Y" or "If X, then Y." Sometimes you may see the modern form, X —> Y, in my comments.
When you see X ≡ Y, you should read "X equivalent to Y" or "X strictly implies Y" or "If and only if X, then Y" or "If X, then Y and if Y, then X" (these forms are sometimes shortened to "iff"). "X ≡ Y" can also be read: "Y is necessary for X and X is sufficient for Y." Occasionally one also sees "X ≡ Y" interpreted as "Y holds just in case X holds" or "Y holds only in case X holds" and the converse, "X holds just in case Y holds." Sometimes my comments use the modern X <—> Y.
For the quantifier all, you will see ( ), as in (x)Fx. In my comments I sometimes use the modern symbol ∀, as in ∀xFx. The existential quantifer ∃, as in ∃xFx, is used in W's text and in my comments. P●Q should be read "P and Q." Often the dot is dropped, as in PQ. Occasionally dots are used instead of parentheses.
6
The general form of truth-function is: [p‾,ξ‾,N(ξ‾)].
See Russell's Introduction for elucidation.
This is the general form of proposition.
6.001
This says nothing else than that every proposition is the result of successive applications of the operation N′(ξ‾) to the elementary propositions.
6.002
If we are given the general form of the way in which a proposition is constructed, then thereby we are also given the general form of the way in which by an operation out of one proposition another can be created.
6.01
The general form of the operation Ω′(η‾) is therefore: [ξ‾,N(ξ‾)]′(η‾)(=[η‾,ξ‾,N(ξ‾)]).
This is the most general form of transition from one proposition to another.
6.02
And thus we come to numbers: I define 6.021
A number is the exponent of an operation.
6.022
The concept number is nothing else than that which is common to all numbers, the general form of a number.
The concept number is the variable number.
And the concept of equality of numbers is the general form of all special equalities of numbers.
6.03
The general form of the cardinal number is: [0,ξ,ξ+1].
6.031
The theory of classes is altogether superfluous in mathematics.
Sets are not superfluous in formal logic, I maintain, since (x)Fx and (∃x)Fx contain the hidden set X, with x ∈ X. A primitive notion of set is required for the building up of logic. Since mathematics is viewed as dependent on logic, the notion of set must be axiomatic in math. I favor calling the quantifier-related sets ur-sets since no set theory can be constructed without basic logic and the two quantifiers, along with the logic operations of negation, disjunction and conjunction (which can be combined into the single operation nand or not-and).
As Paul Benacerraf and Hilary Putnam say in their Introduction to Philosophy of Mathematics, Selected Readings (Prentice-Hall 1964),
This is connected with the fact that the generality which we need in mathematics is not the accidental one.
A mathematician would today argue that, given the axioms, a set theory is a form of mathematics. It deals with precise abstract relations, which is what any mathematical area entails.
6.1
The propositions of logic are tautologies.
I suppose he means by this the axioms.
6.11
The propositions of logic therefore say nothing. (They are the analytical propositions.)
6.111
Theories which make a proposition of logic appear substantial are always false. One could e.g. believe that the words “true” and “false” signify two properties among other properties, and then it would appear as a remarkable fact that every proposition possesses one of these properties. This now by no means appears self-evident, no more so than the proposition “All roses are either yellow or red” would seem even if it were true. Indeed our proposition now gets quite the character of a proposition of natural science and this is a certain symptom of its being falsely understood.
6.112
The correct explanation of logical propositions must give them a peculiar position among all propositions.
6.113
It is the characteristic mark of logical propositions that one can perceive in the symbol alone that they are true; and this fact contains in itself the whole philosophy of logic. And so also it is one of the most important facts that the truth or falsehood of non-logical propositions can not be recognized from the propositions alone.
This follows from the fact that the symbol, say P, represents a formula (well-formed formula) or relation without specifying the particulars. Thus, P ⊃ P and PQ ⊃ P are viewed as basic laws of thought. One can justify them further (for example, see Rosser, Logic, 1953), but at some point some axioms are "obvious" reflections of proper thought. So P is the symbol for the general formula or general relation. P = aRb means that Po = aRb. That is, aRb represents an instance of P. aRb may be empirical or it may result from analysis, as in R means "less than." 1R2 is true; 2R1 is false; greenR5 is meaningless.
6.12
The fact that the propositions of logic are tautologies shows the formal—logical—properties of language, of the world.
That its constituent parts connected together in this way give a tautology characterizes the logic of its constituent parts.
In order that propositions connected together in a definite way may give a tautology they must have definite properties of structure. That they give a tautology when so connected shows therefore that they possess these properties of structure.
6.1201
That e.g. the propositions “p” and “~p” in the connection “~(p.~p)” give a tautology shows that they contradict one another. That the propositions “p⊃q”, “p” and “q” connected together in the form “(p⊃q).(p):⊃:(q)” give a tautology shows that q follows from p and p⊃q. That “(x).fx:⊃:fa” is a tautology shows that fa follows from (x).fx, etc. etc.
One might say that ~(p.~p) is a necessary axiom of logic. It says that contradiction is not permitted. We also need a truth value axiom, I would say, as in: "Any P carries a value of true xor false even if that value can't be determined." Or, "Any P carries a value of T (or 1) xor ~T (or 0) xor U (or undecidable, 2)."†
6.1202
It is clear that we could have used for this purpose contradictions instead of tautologies.
6.1203
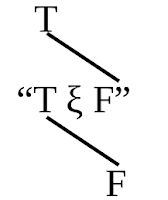
In order to recognize a tautology as such, we can, in cases in which no sign of generality occurs in the tautology, make use of the following intuitive method: I write instead of “p”, “q”, “r”, etc., “TpF”, “TqF”, “TrF”, etc. The truth-combinations I express by brackets, e.g.: The propositions TpF and TqF, connected by brackets above and below. and the coordination of the truth or falsity of the whole proposition with the truth-combinations of the truth-arguments by lines in the following way: The propositions TpF and TqF, connected by brackets above and below; F is connected from above, and T from below. This sign, for example, would therefore present the proposition p⊃q. Now I will proceed to inquire whether such a proposition as ~(p.~p) (The Law of Contradiction) is a tautology. The form “~ξ” is written in our notation The proposition T ξ F, with T connected from above and F from below. the form “ξ.η” thus:— The propositions TξF and TηF, with braces above and below; T is connected from above, and F from below. Hence the proposition ~(p.~q) runs thus:— The previous three figures merged.
If here we put “p” instead of “q” and examine the combination of the outermost T and F with the innermost, it is seen that the truth of the whole proposition is coordinated with all the truth-combinations of its argument, its falsity with none of the truth-combinations.
6.121
The propositions of logic demonstrate the logical properties of propositions, by combining them into propositions which say nothing.
This method could be called a zero-method. In a logical proposition propositions are brought into equilibrium with one another, and the state of equilibrium then shows how these propositions must be logically constructed.
6.122
Whence it follows that we can get on without logical propositions, for we can recognize in an adequate notation the formal properties of the propositions by mere inspection.
6.1221
If for example two propositions “p” and “q” give a tautology in the connection “p⊃q”, then it is clear that q follows from p.
E.g. that “q” follows from “p⊃q.p” we see from these two propositions themselves, but we can also show it by combining them to “q” follows from “p⊃q.p:⊃:q” and then showing that this is a tautology.
6.1222
This throws light on the question why logical propositions can no more be empirically confirmed than they can be empirically refuted. Not only must a proposition of logic be incapable of being contradicted by any possible experience, but it must also be incapable of being confirmed by any such.
6.1223
It now becomes clear why we often feel as though “logical truths” must be “postulated” by us. We can in fact postulate them in so far as we can postulate an adequate notation.
6.1224
It also becomes clear why logic has been called the theory of forms and of inference.
6.123
It is clear that the laws of logic cannot themselves obey further logical laws.
(There is not, as Russell supposed, for every “type” a special law of contradiction; but one is sufficient, since it is not applied to itself.)
6.1231
The mark of logical propositions is not their general validity.
To be general is only to be accidentally valid for all things. An ungeneralized proposition can be tautologous just as well as a generalized one.
6.1232
Logical general validity, we could call essential as opposed to accidental general validity, e.g. of the proposition “all men are mortal.” Propositions like Russell’s “axiom of reducibility” are not logical propositions, and this explains our feeling that, if true, they can only be true by a happy chance.
6.1233
We can imagine a world in which the axiom of reducibility is not valid. But it is clear that logic has nothing to do with the question whether our world is really of this kind or not.
6.124
The logical propositions describe the scaffolding of the world, or rather they present it. They “treat” of nothing. They presuppose that names have meaning, and that elementary propositions have sense. And this is their connection with the world. It is clear that it must show something about the world that certain combinations of symbols—which essentially have a definite character—are tautologies. Herein lies the decisive point. We said that in the symbols which we use something is arbitrary, something not. In logic only this expresses: but this means that in logic it is not we who express, by means of signs, what we want, but in logic the nature of the essentially necessary signs itself asserts. That is to say, if we know the logical syntax of any sign language, then all the propositions of logic are already given.
6.125
It is possible, also with the old conception of logic, to give at the outset a description of all “true” logical propositions.
6.1251
Hence there can never be surprises in logic.
6.126
Whether a proposition belongs to logic can be calculated by calculating the logical properties of the symbol.
And this we do when we prove a logical proposition. For without troubling ourselves about a sense and a meaning, we form the logical propositions out of others by mere symbolic rules.
We prove a logical proposition by creating it out of other logical propositions by applying in succession certain operations, which again generate tautologies out of the first. (And from a tautology only tautologies follow.)
Naturally this way of showing that its propositions are tautologies is quite unessential to logic. Because the propositions, from which the proof starts, must show without proof that they are tautologies.
6.1261
In logic process and result are equivalent. (Therefore no surprises.)
6.1262
Proof in logic is only a mechanical expedient to facilitate the recognition of tautology, where it is complicated.
6.1263
It would be too remarkable, if one could prove a significant proposition logically from another, and a logical proposition also. It is clear from the beginning that the logical proof of a significant proposition and the proof in logic must be two quite different things.
6.1264
The significant proposition asserts something, and its proof shows that it is so; in logic every proposition is the form of a proof.
Every proposition of logic is a modus ponens presented in signs. (And the modus ponens can not be expressed by a proposition.)
6.1265
Logic can always be conceived to be such that every proposition is its own proof.
6.127
All propositions of logic are of equal rank; there are not some which are essentially primitive and others deduced from there.
Every tautology itself shows that it is a tautology.
6.1271
It is clear that the number of “primitive propositions of logic” is arbitrary, for we could deduce logic from one primitive proposition by simply forming, for example, the logical produce of Frege’s primitive propositions. (Frege would perhaps say that this would no longer be immediately self-evident. But it is remarkable that so exact a thinker as Frege should have appealed to the degree of self-evidence as the criterion of a logical proposition.)
6.13
Logic is not a theory but a reflection of the world.
Logic is transcendental.
6.2
Mathematics is a logical method.
The propositions of mathematics are equations, and therefore pseudo-propositions.
In Euclidean geometry, infinitely extended parallel lines never meet. Is this proposition an equation or is the proposition talking about an equality?
6.21
Mathematical propositions express no thoughts.
6.211 In life it is never a mathematical proposition which we need, but we use mathematical propositions only in order to infer from propositions which do not belong to mathematics to others which equally do not belong to mathematics.
(In philosophy the question “Why do we really use that word, that proposition?” constantly leads to valuable results.)
6.22
The logic of the world which the propositions of logic show in tautologies, mathematics shows in equations.
6.23
If two expressions are connected by the sign of equality, this means that they can be substituted for one another. But whether this is the case must show itself in the two expressions themselves.
It characterizes the logical form of two expressions, that they can be substituted for one another.
6.231
It is a property of affirmation that it can be conceived as double denial.
It is a property of “1+1+1+1” that it can be conceived as “(1+1)+(1+1)”.
6.232
Frege says that these expressions have the same meaning but different senses.
But what is essential about equation is that it is not necessary in order to show that both expressions, which are connected by the sign of equality, have the same meaning: for this can be perceived from the two expressions themselves.
6.2321
And, that the propositions of mathematics can be proved means nothing else than that their correctness can be seen without our having to compare what they express with the facts as regards correctness.
6.2322
The identity of the meaning of two expressions cannot be asserted. For in order to be able to assert anything about their meaning, I must know their meaning, and if I know their meaning, I know whether they mean the same or something different.
6.2323
The equation characterizes only the standpoint from which I consider the two expressions, that is to say the standpoint of their equality of meaning.
6.233
To the question whether we need intuition for the solution of mathematical problems it must be answered that language itself here supplies the necessary intuition.
6.2331
The process of calculation brings about just this intuition.
Calculation is not an experiment.
6.234
Mathematics is a method of logic.
6.2341
The essential of mathematical method is working with equations. On this method depends the fact that every proposition of mathematics must be self-evident.
6.24
The method by which mathematics arrives at its equations is the method of substitution.
For equations express the substitutability of two expressions, and we proceed from a number of equations to new equations, replacing expressions by others in accordance with the equations.
6.241
Thus the proof of the proposition 2×2=4 runs:
6.3
Logical research means the investigation of all regularity. And outside logic all is accident.
6.31
The so-called law of induction cannot in any case be a logical law, for it is obviously a significant proposition.—And therefore it cannot be a law a priori either.
6.32
The law of causality is not a law but the form of a law.2
6.321
“Law of Causality” is a class name. And as in mechanics there are, for instance, minimum-laws, such as that of least actions, so in physics there are causal laws, laws of the causality form.
6.3211
Men had indeed an idea that there must be a “law of least action,” before they knew exactly how it ran. (Here, as always, the a priori certain proves to be something purely logical.)
6.33
We do not believe a priori in a law of conservation, but we know a priori the possibility of a logical form. 6.34 All propositions, such as the law of causation, the law of continuity in nature, the law of least expenditure in nature, etc. etc., all these are a priori intuitions of possible forms of the propositions of science. 6.341 Newtonian mechanics, for example, brings the description of the universe to a unified form. Let us imagine a white surface with irregular black spots. We now say: Whatever kind of picture these make I can always get as near as I like to its description, if I cover the surface with a sufficiently fine square network and now say of every square that it is white or black. In this way I shall have brought the description of the surface to a unified form. This form is arbitrary, because I could have applied with equal success a net with a triangular or hexagonal mesh. It can happen that the description would have been simpler with the aid of a triangular mesh; that is to say we might have described the surface more accurately with a triangular, and coarser, than with the finer square mesh, or vice versa, and so on. To the different networks correspond different systems of describing the world. Mechanics determine a form of description by saying: All propositions in the description of the world must be obtained in a given way from a number of given propositions—the mechanical axioms. It thus provides the bricks for building the edifice of science, and says: Whatever building thou wouldst erect, thou shalt construct it in some manner with these bricks and these alone.
(As with the system of numbers one must be able to write down any arbitrary number, so with the system of mechanics one must be able to write down any arbitrary physical proposition.)
6.342 And now we see the relative position of logic and mechanics. (We could construct the network out of figures of different kinds, as out of triangles and hexagons together.) That a picture like that instanced above can be described by a network of a given form asserts nothing about the picture. (For this holds of every picture of this kind.) But this does characterize the picture, the fact, namely, that it can be completely described by a definite net of definite fineness.
So too the fact that it can be described by Newtonian mechanics asserts nothing about the world; but this asserts something, namely, that it can be described in that particular way in which as a matter of fact it is described. The fact, too, that it can be described more simply by one system of mechanics than by another says something about the world.
6.343
Mechanics is an attempt to construct according to a single plan all true propositions which we need for the description of the world.
6.3431
Through their whole logical apparatus the physical laws still speak of the objects of the world.
6.3432
We must not forget that the description of the world by mechanics is always quite general. There is, for example, never any mention of particular material points in it, but always only of some points or other.
6.35
Although the spots in our picture are geometrical figures, geometry can obviously say nothing about their actual form and position. But the network is purely geometrical, and all its properties can be given a priori.
Laws, like the law of causation, etc., treat of the network and not what the network describes.
6.36
If there were a law of causality, it might run: “There are natural laws.”
But that can clearly not be said: it shows itself.
6.361
In the terminology of Hertz we might say: Only uniform connections are thinkable.
6.3611
We cannot compare any process with the “passage of time”—there is no such thing—but only with another process (say, with the movement of the chronometer).
Hence the description of the temporal sequence of events is only possible if we support ourselves on another process.
It is exactly analogous for space. When, for example, we say that neither of two events (which mutually exclude one another) can occur, because there is no cause why the one should occur rather than the other, it is really a matter of our being unable to describe one of the two events unless there is some sort of asymmetry. And if there is such an asymmetry, we can regard this as the cause of the occurrence of the one and of the nonoccurrence of the other.
6.36111
The Kantian problem of the right and left hand which cannot be made to cover one another already exists in the plane, and even in one-dimensional space; where the two congruent figures a and b cannot be made to cover one another without moving them out of this space. The right and left hand are in fact completely congruent. And the fact that they cannot be made to cover one another has nothing to do with it.
A right-hand glove could be put on a left hand if it could be turned round in four-dimensional space.
A right-hand glove could be put on a left hand if it could be turned round in four-dimensional space.
6.362
What can be described can happen too, and what is excluded by the law of causality cannot be described.
6.363
The process of induction is the process of assuming the simplest law that can be made to harmonize with our experience.
6.3631
This process, however, has no logical foundation but only a psychological one. It is clear that there are no grounds for believing that the simplest course of events will really happen.
6.36311
That the sun will rise tomorrow, is an hypothesis; and that means that we do not know whether it will rise.
6.37
A necessity for one thing to happen because another has happened does not exist. There is only logical necessity.
6.371
At the basis of the whole modern view of the world lies the illusion that the so-called laws of nature are the explanations of natural phenomena.
6.372
So people stop short at natural laws as something unassailable, as did the ancients at God and Fate.
And they are both right and wrong. But the ancients were clearer, in so far as they recognized one clear terminus, whereas the modern system makes it appear as though everything were explained.
6.373
The world is independent of my will.
6.374
Even if everything we wished were to happen, this would only be, so to speak, a favour of fate, for there is no logical connection between will and world, which would guarantee this, and the assumed physical connection itself we could not again will.
6.375
As there is only a logical necessity, so there is only a logical impossibility.
6.3751
For two colours, e.g. to be at one place in the visual field, is impossible, logically impossible, for it is excluded by the logical structure of colour.
Let us consider how this contradiction presents itself in physics. Somewhat as follows: That a particle cannot at the same time have two velocities, i.e. that at the same time it cannot be in two places, i.e. that particles in different places at the same time cannot be identical.
It is clear that the logical product of two elementary propositions can neither be a tautology nor a contradiction. The assertion that a point in the visual field has two different colours at the same time, is a contradiction.
6.4
All propositions are of equal value.
6.41
The sense of the world must lie outside the world. In the world everything is as it is and happens as it does happen. In it there is no value—and if there were, it would be of no value.
If there is a value which is of value, it must lie outside all happening and being-so. For all happening and being-so is accidental.
What makes it non-accidental cannot lie in the world, for otherwise this would again be accidental.
It must lie outside the world.
6.42
Hence also there can be no ethical propositions.
Propositions cannot express anything higher.
6.421
It is clear that ethics cannot be expressed.
Ethics is transcendental.
(Ethics and aesthetics are one.)
6.422
The first thought in setting up an ethical law of the form “thou shalt …” is: And what if I do not do it? But it is clear that ethics has nothing to do with punishment and reward in the ordinary sense. This question as to the consequences of an action must therefore be irrelevant. At least these consequences will not be events. For there must be something right in that formulation of the question. There must be some sort of ethical reward and ethical punishment, but this must lie in the action itself.
(And this is clear also that the reward must be something acceptable, and the punishment something unacceptable.)
6.423
Of the will as the subject of the ethical we cannot speak.
And the will as a phenomenon is only of interest to psychology.
6.43
If good or bad willing changes the world, it can only change the limits of the world, not the facts; not the things that can be expressed in language.
In brief, the world must thereby become quite another, it must so to speak wax or wane as a whole.
The world of the happy is quite another than that of the unhappy.
6.431
As in death, too, the world does not change, but ceases.
6.4311
Death is not an event of life. Death is not lived through.
If by eternity is understood not endless temporal duration but timelessness, then he lives eternally who lives in the present.
Our life is endless in the way that our visual field is without limit.
6.4312
The temporal immortality of the human soul, that is to say, its eternal survival also after death, is not only in no way guaranteed, but this assumption in the first place will not do for us what we always tried to make it do. Is a riddle solved by the fact that I survive forever? Is this eternal life not as enigmatic as our present one? The solution of the riddle of life in space and time lies outside space and time.
(It is not problems of natural science which have to be solved.)
6.432
How the world is, is completely indifferent for what is higher. God does not reveal himself in the world.
He knows this -- how? Divine revelation?
6.4321
The facts all belong only to the task and not to its performance.
6.44
Not how the world is, is the mystical, but that it is.
6.45
The contemplation of the world sub specie aeterni is its contemplation as a limited whole.
The feeling that the world is a limited whole is the mystical feeling.
6.5
For an answer which cannot be expressed the question too cannot be expressed.
The riddle does not exist.
If a question can be put at all, then it can also be answered.
6.51
Scepticism is not irrefutable, but palpably senseless, if it would doubt where a question cannot be asked.
For doubt can only exist where there is a question; a question only where there is an answer, and this only where something can be said.
6.52
We feel that even if all possible scientific questions be answered, the problems of life have still not been touched at all. Of course there is then no question left, and just this is the answer.
6.521
The solution of the problem of life is seen in the vanishing of this problem.
(Is not this the reason why men to whom after long doubting the sense of life became clear, could not then say wherein this sense consisted?)
6.522
There is indeed the inexpressible. This shows itself; it is the mystical.
6.53
The right method of philosophy would be this: To say nothing except what can be said, i.e. the propositions of natural science, i.e. something that has nothing to do with philosophy: and then always, when someone else wished to say something metaphysical, to demonstrate to him that he had given no meaning to certain signs in his propositions. This method would be unsatisfying to the other—he would not have the feeling that we were teaching him philosophy—but it would be the only strictly correct method.
6.54
My propositions are elucidatory in this way: he who understands me finally recognizes them as senseless, when he has climbed out through them, on them, over them. (He must so to speak throw away the ladder, after he has climbed up on it.)
He must surmount these propositions; then he sees the world rightly.
The general form of truth-function is: [p‾,ξ‾,N(ξ‾)].
See Russell's Introduction for elucidation.
6.001
This says nothing else than that every proposition is the result of successive applications of the operation N′(ξ‾) to the elementary propositions.
6.002
If we are given the general form of the way in which a proposition is constructed, then thereby we are also given the general form of the way in which by an operation out of one proposition another can be created.
6.01
The general form of the operation Ω′(η‾) is therefore: [ξ‾,N(ξ‾)]′(η‾)(=[η‾,ξ‾,N(ξ‾)]).
This is the most general form of transition from one proposition to another.
6.02
And thus we come to numbers: I define 6.021
A number is the exponent of an operation.
6.022
The concept number is nothing else than that which is common to all numbers, the general form of a number.
The concept number is the variable number.
And the concept of equality of numbers is the general form of all special equalities of numbers.
6.03
The general form of the cardinal number is: [0,ξ,ξ+1].
6.031
The theory of classes is altogether superfluous in mathematics.
Sets are not superfluous in formal logic, I maintain, since (x)Fx and (∃x)Fx contain the hidden set X, with x ∈ X. A primitive notion of set is required for the building up of logic. Since mathematics is viewed as dependent on logic, the notion of set must be axiomatic in math. I favor calling the quantifier-related sets ur-sets since no set theory can be constructed without basic logic and the two quantifiers, along with the logic operations of negation, disjunction and conjunction (which can be combined into the single operation nand or not-and).
As Paul Benacerraf and Hilary Putnam say in their Introduction to Philosophy of Mathematics, Selected Readings (Prentice-Hall 1964),
Logicists [in particular Gottlob Frege, Bertrand Russell and A.N. Whitehead] did not reduce all of mathematics to elementary logic, but they did reduce mathematics to elementary logic plus the theory of properties (or sets), properties of properties, properties of properties of properties, and so on. Thus if property theory (or set theory) may be counted as part of logic, mathematics is reducible to logic.
A mathematician would today argue that, given the axioms, a set theory is a form of mathematics. It deals with precise abstract relations, which is what any mathematical area entails.
The propositions of logic are tautologies.
I suppose he means by this the axioms.
The propositions of logic therefore say nothing. (They are the analytical propositions.)
6.111
Theories which make a proposition of logic appear substantial are always false. One could e.g. believe that the words “true” and “false” signify two properties among other properties, and then it would appear as a remarkable fact that every proposition possesses one of these properties. This now by no means appears self-evident, no more so than the proposition “All roses are either yellow or red” would seem even if it were true. Indeed our proposition now gets quite the character of a proposition of natural science and this is a certain symptom of its being falsely understood.
6.112
The correct explanation of logical propositions must give them a peculiar position among all propositions.
6.113
It is the characteristic mark of logical propositions that one can perceive in the symbol alone that they are true; and this fact contains in itself the whole philosophy of logic. And so also it is one of the most important facts that the truth or falsehood of non-logical propositions can not be recognized from the propositions alone.
This follows from the fact that the symbol, say P, represents a formula (well-formed formula) or relation without specifying the particulars. Thus, P ⊃ P and PQ ⊃ P are viewed as basic laws of thought. One can justify them further (for example, see Rosser, Logic, 1953), but at some point some axioms are "obvious" reflections of proper thought. So P is the symbol for the general formula or general relation. P = aRb means that Po = aRb. That is, aRb represents an instance of P. aRb may be empirical or it may result from analysis, as in R means "less than." 1R2 is true; 2R1 is false; greenR5 is meaningless.
The fact that the propositions of logic are tautologies shows the formal—logical—properties of language, of the world.
That its constituent parts connected together in this way give a tautology characterizes the logic of its constituent parts.
In order that propositions connected together in a definite way may give a tautology they must have definite properties of structure. That they give a tautology when so connected shows therefore that they possess these properties of structure.
6.1201
That e.g. the propositions “p” and “~p” in the connection “~(p.~p)” give a tautology shows that they contradict one another. That the propositions “p⊃q”, “p” and “q” connected together in the form “(p⊃q).(p):⊃:(q)” give a tautology shows that q follows from p and p⊃q. That “(x).fx:⊃:fa” is a tautology shows that fa follows from (x).fx, etc. etc.
One might say that ~(p.~p) is a necessary axiom of logic. It says that contradiction is not permitted. We also need a truth value axiom, I would say, as in: "Any P carries a value of true xor false even if that value can't be determined." Or, "Any P carries a value of T (or 1) xor ~T (or 0) xor U (or undecidable, 2)."†
It is clear that we could have used for this purpose contradictions instead of tautologies.
6.1203
In order to recognize a tautology as such, we can, in cases in which no sign of generality occurs in the tautology, make use of the following intuitive method: I write instead of “p”, “q”, “r”, etc., “TpF”, “TqF”, “TrF”, etc. The truth-combinations I express by brackets, e.g.: The propositions TpF and TqF, connected by brackets above and below. and the coordination of the truth or falsity of the whole proposition with the truth-combinations of the truth-arguments by lines in the following way: The propositions TpF and TqF, connected by brackets above and below; F is connected from above, and T from below. This sign, for example, would therefore present the proposition p⊃q. Now I will proceed to inquire whether such a proposition as ~(p.~p) (The Law of Contradiction) is a tautology. The form “~ξ” is written in our notation The proposition T ξ F, with T connected from above and F from below. the form “ξ.η” thus:— The propositions TξF and TηF, with braces above and below; T is connected from above, and F from below. Hence the proposition ~(p.~q) runs thus:— The previous three figures merged.
If here we put “p” instead of “q” and examine the combination of the outermost T and F with the innermost, it is seen that the truth of the whole proposition is coordinated with all the truth-combinations of its argument, its falsity with none of the truth-combinations.
6.121
The propositions of logic demonstrate the logical properties of propositions, by combining them into propositions which say nothing.
This method could be called a zero-method. In a logical proposition propositions are brought into equilibrium with one another, and the state of equilibrium then shows how these propositions must be logically constructed.
6.122
Whence it follows that we can get on without logical propositions, for we can recognize in an adequate notation the formal properties of the propositions by mere inspection.
6.1221
If for example two propositions “p” and “q” give a tautology in the connection “p⊃q”, then it is clear that q follows from p.
E.g. that “q” follows from “p⊃q.p” we see from these two propositions themselves, but we can also show it by combining them to “q” follows from “p⊃q.p:⊃:q” and then showing that this is a tautology.
6.1222
This throws light on the question why logical propositions can no more be empirically confirmed than they can be empirically refuted. Not only must a proposition of logic be incapable of being contradicted by any possible experience, but it must also be incapable of being confirmed by any such.
6.1223
It now becomes clear why we often feel as though “logical truths” must be “postulated” by us. We can in fact postulate them in so far as we can postulate an adequate notation.
6.1224
It also becomes clear why logic has been called the theory of forms and of inference.
6.123
It is clear that the laws of logic cannot themselves obey further logical laws.
(There is not, as Russell supposed, for every “type” a special law of contradiction; but one is sufficient, since it is not applied to itself.)
6.1231
The mark of logical propositions is not their general validity.
To be general is only to be accidentally valid for all things. An ungeneralized proposition can be tautologous just as well as a generalized one.
6.1232
Logical general validity, we could call essential as opposed to accidental general validity, e.g. of the proposition “all men are mortal.” Propositions like Russell’s “axiom of reducibility” are not logical propositions, and this explains our feeling that, if true, they can only be true by a happy chance.
6.1233
We can imagine a world in which the axiom of reducibility is not valid. But it is clear that logic has nothing to do with the question whether our world is really of this kind or not.
6.124
The logical propositions describe the scaffolding of the world, or rather they present it. They “treat” of nothing. They presuppose that names have meaning, and that elementary propositions have sense. And this is their connection with the world. It is clear that it must show something about the world that certain combinations of symbols—which essentially have a definite character—are tautologies. Herein lies the decisive point. We said that in the symbols which we use something is arbitrary, something not. In logic only this expresses: but this means that in logic it is not we who express, by means of signs, what we want, but in logic the nature of the essentially necessary signs itself asserts. That is to say, if we know the logical syntax of any sign language, then all the propositions of logic are already given.
6.125
It is possible, also with the old conception of logic, to give at the outset a description of all “true” logical propositions.
6.1251
Hence there can never be surprises in logic.
6.126
Whether a proposition belongs to logic can be calculated by calculating the logical properties of the symbol.
And this we do when we prove a logical proposition. For without troubling ourselves about a sense and a meaning, we form the logical propositions out of others by mere symbolic rules.
We prove a logical proposition by creating it out of other logical propositions by applying in succession certain operations, which again generate tautologies out of the first. (And from a tautology only tautologies follow.)
Naturally this way of showing that its propositions are tautologies is quite unessential to logic. Because the propositions, from which the proof starts, must show without proof that they are tautologies.
6.1261
In logic process and result are equivalent. (Therefore no surprises.)
6.1262
Proof in logic is only a mechanical expedient to facilitate the recognition of tautology, where it is complicated.
6.1263
It would be too remarkable, if one could prove a significant proposition logically from another, and a logical proposition also. It is clear from the beginning that the logical proof of a significant proposition and the proof in logic must be two quite different things.
6.1264
The significant proposition asserts something, and its proof shows that it is so; in logic every proposition is the form of a proof.
Every proposition of logic is a modus ponens presented in signs. (And the modus ponens can not be expressed by a proposition.)
6.1265
Logic can always be conceived to be such that every proposition is its own proof.
6.127
All propositions of logic are of equal rank; there are not some which are essentially primitive and others deduced from there.
Every tautology itself shows that it is a tautology.
6.1271
It is clear that the number of “primitive propositions of logic” is arbitrary, for we could deduce logic from one primitive proposition by simply forming, for example, the logical produce of Frege’s primitive propositions. (Frege would perhaps say that this would no longer be immediately self-evident. But it is remarkable that so exact a thinker as Frege should have appealed to the degree of self-evidence as the criterion of a logical proposition.)
6.13
Logic is not a theory but a reflection of the world.
Logic is transcendental.
6.2
Mathematics is a logical method.
The propositions of mathematics are equations, and therefore pseudo-propositions.
In Euclidean geometry, infinitely extended parallel lines never meet. Is this proposition an equation or is the proposition talking about an equality?
Mathematical propositions express no thoughts.
6.211 In life it is never a mathematical proposition which we need, but we use mathematical propositions only in order to infer from propositions which do not belong to mathematics to others which equally do not belong to mathematics.
(In philosophy the question “Why do we really use that word, that proposition?” constantly leads to valuable results.)
6.22
The logic of the world which the propositions of logic show in tautologies, mathematics shows in equations.
6.23
If two expressions are connected by the sign of equality, this means that they can be substituted for one another. But whether this is the case must show itself in the two expressions themselves.
It characterizes the logical form of two expressions, that they can be substituted for one another.
6.231
It is a property of affirmation that it can be conceived as double denial.
It is a property of “1+1+1+1” that it can be conceived as “(1+1)+(1+1)”.
6.232
Frege says that these expressions have the same meaning but different senses.
But what is essential about equation is that it is not necessary in order to show that both expressions, which are connected by the sign of equality, have the same meaning: for this can be perceived from the two expressions themselves.
6.2321
And, that the propositions of mathematics can be proved means nothing else than that their correctness can be seen without our having to compare what they express with the facts as regards correctness.
6.2322
The identity of the meaning of two expressions cannot be asserted. For in order to be able to assert anything about their meaning, I must know their meaning, and if I know their meaning, I know whether they mean the same or something different.
6.2323
The equation characterizes only the standpoint from which I consider the two expressions, that is to say the standpoint of their equality of meaning.
6.233
To the question whether we need intuition for the solution of mathematical problems it must be answered that language itself here supplies the necessary intuition.
6.2331
The process of calculation brings about just this intuition.
Calculation is not an experiment.
6.234
Mathematics is a method of logic.
6.2341
The essential of mathematical method is working with equations. On this method depends the fact that every proposition of mathematics must be self-evident.
6.24
The method by which mathematics arrives at its equations is the method of substitution.
For equations express the substitutability of two expressions, and we proceed from a number of equations to new equations, replacing expressions by others in accordance with the equations.
6.241
Thus the proof of the proposition 2×2=4 runs:
6.3
Logical research means the investigation of all regularity. And outside logic all is accident.
6.31
The so-called law of induction cannot in any case be a logical law, for it is obviously a significant proposition.—And therefore it cannot be a law a priori either.
6.32
The law of causality is not a law but the form of a law.2
6.321
“Law of Causality” is a class name. And as in mechanics there are, for instance, minimum-laws, such as that of least actions, so in physics there are causal laws, laws of the causality form.
6.3211
Men had indeed an idea that there must be a “law of least action,” before they knew exactly how it ran. (Here, as always, the a priori certain proves to be something purely logical.)
6.33
We do not believe a priori in a law of conservation, but we know a priori the possibility of a logical form. 6.34 All propositions, such as the law of causation, the law of continuity in nature, the law of least expenditure in nature, etc. etc., all these are a priori intuitions of possible forms of the propositions of science. 6.341 Newtonian mechanics, for example, brings the description of the universe to a unified form. Let us imagine a white surface with irregular black spots. We now say: Whatever kind of picture these make I can always get as near as I like to its description, if I cover the surface with a sufficiently fine square network and now say of every square that it is white or black. In this way I shall have brought the description of the surface to a unified form. This form is arbitrary, because I could have applied with equal success a net with a triangular or hexagonal mesh. It can happen that the description would have been simpler with the aid of a triangular mesh; that is to say we might have described the surface more accurately with a triangular, and coarser, than with the finer square mesh, or vice versa, and so on. To the different networks correspond different systems of describing the world. Mechanics determine a form of description by saying: All propositions in the description of the world must be obtained in a given way from a number of given propositions—the mechanical axioms. It thus provides the bricks for building the edifice of science, and says: Whatever building thou wouldst erect, thou shalt construct it in some manner with these bricks and these alone.
(As with the system of numbers one must be able to write down any arbitrary number, so with the system of mechanics one must be able to write down any arbitrary physical proposition.)
6.342 And now we see the relative position of logic and mechanics. (We could construct the network out of figures of different kinds, as out of triangles and hexagons together.) That a picture like that instanced above can be described by a network of a given form asserts nothing about the picture. (For this holds of every picture of this kind.) But this does characterize the picture, the fact, namely, that it can be completely described by a definite net of definite fineness.
So too the fact that it can be described by Newtonian mechanics asserts nothing about the world; but this asserts something, namely, that it can be described in that particular way in which as a matter of fact it is described. The fact, too, that it can be described more simply by one system of mechanics than by another says something about the world.
6.343
Mechanics is an attempt to construct according to a single plan all true propositions which we need for the description of the world.
6.3431
Through their whole logical apparatus the physical laws still speak of the objects of the world.
6.3432
We must not forget that the description of the world by mechanics is always quite general. There is, for example, never any mention of particular material points in it, but always only of some points or other.
6.35
Although the spots in our picture are geometrical figures, geometry can obviously say nothing about their actual form and position. But the network is purely geometrical, and all its properties can be given a priori.
Laws, like the law of causation, etc., treat of the network and not what the network describes.
6.36
If there were a law of causality, it might run: “There are natural laws.”
But that can clearly not be said: it shows itself.
6.361
In the terminology of Hertz we might say: Only uniform connections are thinkable.
6.3611
We cannot compare any process with the “passage of time”—there is no such thing—but only with another process (say, with the movement of the chronometer).
Hence the description of the temporal sequence of events is only possible if we support ourselves on another process.
It is exactly analogous for space. When, for example, we say that neither of two events (which mutually exclude one another) can occur, because there is no cause why the one should occur rather than the other, it is really a matter of our being unable to describe one of the two events unless there is some sort of asymmetry. And if there is such an asymmetry, we can regard this as the cause of the occurrence of the one and of the nonoccurrence of the other.
6.36111
The Kantian problem of the right and left hand which cannot be made to cover one another already exists in the plane, and even in one-dimensional space; where the two congruent figures a and b cannot be made to cover one another without moving them out of this space. The right and left hand are in fact completely congruent. And the fact that they cannot be made to cover one another has nothing to do with it.
A right-hand glove could be put on a left hand if it could be turned round in four-dimensional space.
A right-hand glove could be put on a left hand if it could be turned round in four-dimensional space.
6.362
What can be described can happen too, and what is excluded by the law of causality cannot be described.
6.363
The process of induction is the process of assuming the simplest law that can be made to harmonize with our experience.
6.3631
This process, however, has no logical foundation but only a psychological one. It is clear that there are no grounds for believing that the simplest course of events will really happen.
6.36311
That the sun will rise tomorrow, is an hypothesis; and that means that we do not know whether it will rise.
6.37
A necessity for one thing to happen because another has happened does not exist. There is only logical necessity.
6.371
At the basis of the whole modern view of the world lies the illusion that the so-called laws of nature are the explanations of natural phenomena.
6.372
So people stop short at natural laws as something unassailable, as did the ancients at God and Fate.
And they are both right and wrong. But the ancients were clearer, in so far as they recognized one clear terminus, whereas the modern system makes it appear as though everything were explained.
6.373
The world is independent of my will.
6.374
Even if everything we wished were to happen, this would only be, so to speak, a favour of fate, for there is no logical connection between will and world, which would guarantee this, and the assumed physical connection itself we could not again will.
6.375
As there is only a logical necessity, so there is only a logical impossibility.
6.3751
For two colours, e.g. to be at one place in the visual field, is impossible, logically impossible, for it is excluded by the logical structure of colour.
Let us consider how this contradiction presents itself in physics. Somewhat as follows: That a particle cannot at the same time have two velocities, i.e. that at the same time it cannot be in two places, i.e. that particles in different places at the same time cannot be identical.
It is clear that the logical product of two elementary propositions can neither be a tautology nor a contradiction. The assertion that a point in the visual field has two different colours at the same time, is a contradiction.
6.4
All propositions are of equal value.
6.41
The sense of the world must lie outside the world. In the world everything is as it is and happens as it does happen. In it there is no value—and if there were, it would be of no value.
If there is a value which is of value, it must lie outside all happening and being-so. For all happening and being-so is accidental.
What makes it non-accidental cannot lie in the world, for otherwise this would again be accidental.
It must lie outside the world.
6.42
Hence also there can be no ethical propositions.
Propositions cannot express anything higher.
6.421
It is clear that ethics cannot be expressed.
Ethics is transcendental.
(Ethics and aesthetics are one.)
6.422
The first thought in setting up an ethical law of the form “thou shalt …” is: And what if I do not do it? But it is clear that ethics has nothing to do with punishment and reward in the ordinary sense. This question as to the consequences of an action must therefore be irrelevant. At least these consequences will not be events. For there must be something right in that formulation of the question. There must be some sort of ethical reward and ethical punishment, but this must lie in the action itself.
(And this is clear also that the reward must be something acceptable, and the punishment something unacceptable.)
6.423
Of the will as the subject of the ethical we cannot speak.
And the will as a phenomenon is only of interest to psychology.
6.43
If good or bad willing changes the world, it can only change the limits of the world, not the facts; not the things that can be expressed in language.
In brief, the world must thereby become quite another, it must so to speak wax or wane as a whole.
The world of the happy is quite another than that of the unhappy.
6.431
As in death, too, the world does not change, but ceases.
6.4311
Death is not an event of life. Death is not lived through.
If by eternity is understood not endless temporal duration but timelessness, then he lives eternally who lives in the present.
Our life is endless in the way that our visual field is without limit.
6.4312
The temporal immortality of the human soul, that is to say, its eternal survival also after death, is not only in no way guaranteed, but this assumption in the first place will not do for us what we always tried to make it do. Is a riddle solved by the fact that I survive forever? Is this eternal life not as enigmatic as our present one? The solution of the riddle of life in space and time lies outside space and time.
(It is not problems of natural science which have to be solved.)
6.432
How the world is, is completely indifferent for what is higher. God does not reveal himself in the world.
He knows this -- how? Divine revelation?
The facts all belong only to the task and not to its performance.
6.44
Not how the world is, is the mystical, but that it is.
6.45
The contemplation of the world sub specie aeterni is its contemplation as a limited whole.
The feeling that the world is a limited whole is the mystical feeling.
6.5
For an answer which cannot be expressed the question too cannot be expressed.
The riddle does not exist.
If a question can be put at all, then it can also be answered.
6.51
Scepticism is not irrefutable, but palpably senseless, if it would doubt where a question cannot be asked.
For doubt can only exist where there is a question; a question only where there is an answer, and this only where something can be said.
6.52
We feel that even if all possible scientific questions be answered, the problems of life have still not been touched at all. Of course there is then no question left, and just this is the answer.
6.521
The solution of the problem of life is seen in the vanishing of this problem.
(Is not this the reason why men to whom after long doubting the sense of life became clear, could not then say wherein this sense consisted?)
6.522
There is indeed the inexpressible. This shows itself; it is the mystical.
6.53
The right method of philosophy would be this: To say nothing except what can be said, i.e. the propositions of natural science, i.e. something that has nothing to do with philosophy: and then always, when someone else wished to say something metaphysical, to demonstrate to him that he had given no meaning to certain signs in his propositions. This method would be unsatisfying to the other—he would not have the feeling that we were teaching him philosophy—but it would be the only strictly correct method.
6.54
My propositions are elucidatory in this way: he who understands me finally recognizes them as senseless, when he has climbed out through them, on them, over them. (He must so to speak throw away the ladder, after he has climbed up on it.)
He must surmount these propositions; then he sees the world rightly.
2. I.e. not the form of one particular law, but of any law of a certain sort. (B. R.)
† . T = 1, ~T = 0, U = 2. The rules for 2 are:
2 + 1 = 2I concede that this interpretation is debatable.
'P is undecidable or true.' P cannot be decided because falsehood is not an option.
2 + 0 = 2
'P is undecidable or false.' P cannot be decided because truth is not an option.
2 + 2 = 2
'P is undecidable or undecidable.' P cannot be decided because it lacks the options of truth and falsehood.
0 + 1 + 2 = 1
'P is false, true or undecidable.' These are all the options; hence P is true.
2*1*0 = 0
'P is undecidable and true and false.' Contradiction,
2*0 = 0
'P is undecidable and false.' Contradiction
2*1 = 0
'P is undecidable and true.' Contradiction.
2*2 = 2
'P is undecidable and undecidable.' A contradiction would make P false, as in 'undecidable and true' or 'undecidable and false.' Thus P is either true or undecidable. But to obtain true, one needs 'true and true.' Hence P is undecidable.
We do not worry about the formulations '0 + 1 = 1' and '0*1 = 0.' That is, though 'undecidable' is not an option, that option may be dropped if there is no reason to call for it.








No comments:
Post a Comment