An objection to Proposition 1 of Tractatus

---

This is a very old essay of mine. I have recently made
minor corrections and improvements.
Though I like its ideas and tenor, I concede that
it is not as cohesive as it ought to be. I certainly would not
write something like this these days.

---

From Wittgenstein's 'Tractatus Logico-Philosophicus,' proposition 1:

1. The world is all that is the case.
1.1 The world is the totality of facts, not of things.
1.11 The world is determined by the facts, and by their being ALL the facts.
1.12 For the totality of facts determines what is the case, and also whatever is not the case.
1.13. The facts in logical space are the world.
1.2 The world divides into facts.
1.21 Each item can be the case or not the case while everything else remains the same.

We include proposition 2.0, which includes a key concept:

2.0 What is the case -- a fact -- is the existence of states of affairs [or, atomic propositions].

According to Ray Monk's astute biography, Ludwig Wittgenstein, the Duty of Genius (Free Press division of Macmillan 1990), Gottlob Frege aggravated Wittgenstein by apparently never getting beyond the first page of 'Tractatus' and quibbling over definitions.

However, it seems to me there is merit in taking exception to the initial assumption, even if perhaps definitions can be clarified (as we know, Wittgenstein later repudiated the theory of pictures that underlay the 'Tractatus'; nevertheless, a great value of 'Tractatus' is the compression of concepts that makes the book a goldmine of topics for discussion).

Before doing that, however, I recast proposition 1 as follows:

1. The world is a theorem.
1.1 The world is the set of all theorems, not of things [a thing requires definition and this definition is either a 'higher' theorem or an axiom]
1.11 and 1.12. The set of all theorems determines what is accepted as true and what is not.
1.13 The set of theorems is the world [redundancy acknowledged].
1.2 A theorem represents a piece of the world.
1.21 Some expressions in the form of theorems are held to be false.
2. It is a theorem -- a true proposition -- that axioms exist.

This world view, founded in Wittgenstein's extensive mining of Russell's 'Principia' and fascination with Russell's paradox is reflected in the following:

Suppose we have a set of axioms (two will do here). We can build all theorems and anti-theorems from the axioms (though not necessarily solve basic philosophical issues).

With p and q as axioms (atomic propositions that can't be durther divided by connectives and other symbols except for vacuous tautologies and contradictions), we can begin:

1. p, 2. ~p
3. q, 4. ~q

and call these 4 statements Level 0 set of theorems and anti-theorems. If we say 'it is true that p is a theorem' or 'it is true that ~p is an anti-theorem' then we must use a higher order system of numbering. That is, such a statement must be numbered in such a way as to indicate that it is a statement about a statement. We now can form set Level 1:

5. p & q [theorem]
6. ~p & ~q [anti-theorem]
7. ~p & q [anti-theorem]
8. p & ~q [anti-theorem]
9. p v q [theorem]
10 ~p v q [theorem]
11. p v ~q [theorem]
12. ~p v ~q [anti-theorem]

Level 2 is composed of all possible combinations of p's, q's and connectives, with Level 1 statements combined with Level 2 statements, being a subset of Level 2.

By wise choice of numbering algorithms, we can associate any positive integer with a statement. Also, the truth value of any statement can be ascertained by the truth table method of analyzing such statements. And, it may be possible to find the truth value of statement n by knowing the truth value of sub-statement m, so that reduction to axioms can be avoided in the interest of efficiency.

I have no objection to trying to establish an abstract system using axioms. But the concept of a single system as having a priori existence gives pause.

If I am to agree with Prop 1.0, I must qualify it by insisting on the presence of a human mind, so that 1.0 then means that there is for each mind a corresponding arena of facts. A 'fact' here is a proposition that is assumed true until the mind decides it is false.

I also don't see how we can bypass the notion of 'culture,' which implies a collective set of beliefs and behaviors which acts as an auxiliary memory for each mind that grows within that culture. The interaction of the minds of course yields the evolution of the culture and its collective memory.

Words and word groups are a means of prompting responses from minds (including one's own mind). It seems that most cultures divide words into noun types and verb types. Verbs that cover common occurrences can be noun-ized as in gerunds.

A word may be seen as an auditory association with a specific set of stimuli. When an early man shouted to alert his group to imminent danger, he was at the doorstep of abstraction. When he discovered that use of specific sounds to denote specific threats permitted better responses by the group, he passed through the door of abstraction.

Still, we are assuming that such men had a sense of time and motion about like our own. Beings that perceive without resort to time would not develop language akin to modern speech forms.

In other words, their world would not be our world.

Even beings with a sense of time might differ in their perception of reality. The concept of 'now' is quite difficult to define. However, 'now' does appear to have different meaning in accord with metabolic rate. The smallest meaningful moment of a fly is possibly below the threshold of meaningful human perception. A fly might respond to a motion that is too short for a human to cognize as a motion.

Similarly, another lifeform might have a 'now' considerably longer than ours, with the ultimate 'now' being, theoretically, eternity. Some mystics claim such a time sense.

The word 'deer' (perhaps it is an atomic proposition) does not prove anything about the phenomenon with which it is associated. Deer exist even if a word for a deer doesn't.

Or does it? They exist for us 'because' they have importance for us. That's why we give it a name.

Consider the eskimo who has numerous words for phenomena all of which we English-speakers name 'snow.' We assume that each of these phenomena is an element of a class named 'snow.' But it cannot be assumed that the eskimo perceives these phenomena as types of a single phenomenon. They might be as different as sails and nails as far as he is concerned.

These phenomena are individually named because they are important to him in the sense that his responses to the sets of stimuli that 'signal' a particular phenomenon potentially affect his survival. (We use 'signal' reservedly because the mind knows of the phenomenon only through the sensors [which MIGHT include unconventional sensors, such as spirit detectors].

Suppose a space alien arrived on earth and was able to locomote through trees as if they were gaseous. That being might have very little idea of the concept of tree. Perhaps if it were some sort of scientist, using special detection methods, it might categorize trees by type. Otherwise, a tree would not be part of its world, a self-sevident fact.

What a human is forced to concede is important, at root, is the recurrence of a stimuli set that the memory associates with a pleasure-pain ratio. The brain can add various pleasure-pain ratios as a means of forecasting a probable result. A stimuli set is normally, but not always, composed of elements closely associated in time. It is when these elements are themselves sets of elements that abstraction occurs.

Much more can be said on the issue of learning. perception and mind but the point I wish to make is that when we come upon logical scenarios, such as syllogisms, we are using a human abstraction or association system that reflects our way of learning and coping with pleasure and pain. The fact that, for example, some pain is not directly physical but is 'worry' does not materially affect my point.

That is, 'reality' is quite subjective, though I have not tried to utterly justify the solipsist point of view. And, if reality is deeply subjective, then the laws of form which seem to describe said reality may well be incomplete. I suggest this issue is behind the rigid determinism of Einstein, Bohm and Deutsch (though Bohm's 'implicate order' is a subtle and useful concept).

Deutsch, for example, is correct to endorse the idea that reality might be far bigger than ordinarily presumed. Yet, it is his faith that reality must be fully deterministic that indicates that he thinks that 'objective reality' (the source of inputs into his mind) can be matched point for point with the perception system that is the reality he apprehends (subjective reality).

For example, his reality requires that if a photon can go to point A or point B, there must be a reason in some larger scheme whereby the photon MUST go to either A or B, even if we are utterly unable to predict the correct point. But this 'scientific' assumption stems from the pleasure-pain ratio for stimuli sets in furtherance of the organism's probability of survival. That is, determinism is rooted in our perceptual apparatus. Even 'unscientific' thinking is determinist. 'Causes' however are perhaps identified as gods, demons, spells and counter-spells.

Determinism rests in our sense of 'passage of time.'

In the quantum area, we can use a 'Russell's paradox' approach to perhaps justify the Copenhagen interpretation.

Let's use a symmetrical photon interferometer. If a single photon passes through and is left undetected in transit, it reliably exits only in one direction. If, detected in transit, detection results in a change in exit direction in 50 percent of trials. That is, the photon as a wave interferes with itself, exiting in a single direction. But once the wave 'collapses' because of detection, its position is irrevocably fixed and so exits in the direction established at detection point A or detection point B.

Deutsch, a disciple of Hugh Everett who proposed the 'many worlds' theory, argues that the universe splits into two nearly-identical universes when the photon seems to arbitrarily choose A or B, and in fact follows path A in Universe A and path B in Universe B.

Yet, we might use the determinism of conservation to argue for the Copenhagen interpretation. That is, we may consider a light wave to have a minimum quantum of energy, which we call a quantum amount. If two detectors intercept this wave, only one detector can respond because a detector can't be activated by half a quantum unit. Half a quantum unit is effectively nothing. Well, why are the detectors activated probablistically, you say? Shouldn't some force determine the choice?

Here is where the issue of reality enters.

From a classical standpoint, determinism requires ENERGY. Event A at time(0) is linked to event B at time(1) by an expenditure of energy. But the energy needed for 'throwing the switch on the logic gate' is not present.

We might argue that a necessary feature of a logically consistent deterministic world view founded on discrete calculations requires that determinism is also discrete (not continuous) and hence limited and hence non-deterministic at the quantum level.

---

This page first posted January 2002

Tractatus 7

7
Whereof one cannot speak, thereof one must be silent.

Ahh, one of those tautologies he speaks of. In any case, I suppose he means there is much that is so deeply impenetrable that we cannot make pictures of it for speech purposes. That is, we cannot speak "aRb" if we don't know a, b or R, though we may have a primitive intuition of such a "fact."

Think of most English-speaking people who have only one or two words for "snow." That is because their survival is not dependent on knowing the fine points of types of snow. Northern indigenous people, on the other hand, have many words to describe snow and need not pass over in silence a discussion of such matters. Similarly, scientists, mathematicians and other specialists have many words to describe technical matters that ordinary people lack.

But more importantly, it is amazing how people can find ways to talk about new things that would have befuddled their forebears. Yet, we may also concede that many people report on religious and spiritual mysteries and ecstasies that cannot be adequately described with words.

One also suspects that W. had run out of steam trying to use a mathematical-logical outlook to abolish all the pesky problems of philosophy. Intuitively he realized that if he continued to dig, he would run up against enigmas that were too difficult to cope with.

Tractatus 6

---

When you see X ⊃ Y, you are to read "X implies Y" or "If X, then Y." Sometimes you may see the modern form, X —> Y, in my comments.
When you see X ≡ Y, you should read "X equivalent to Y" or "X strictly implies Y" or "If and only if X, then Y" or "If X, then Y and if Y, then X" (these forms are sometimes shortened to "iff"). "X ≡ Y" can also be read: "Y is necessary for X and X is sufficient for Y." Occasionally one also sees "X ≡ Y" interpreted as "Y holds just in case X holds" or "Y holds only in case X holds" and the converse, "X holds just in case Y holds." Sometimes my comments use the modern X <—> Y.
For the quantifier all, you will see ( ), as in (x)Fx. In my comments I sometimes use the modern symbol ∀, as in ∀xFx. The existential quantifer ∃, as in ∃xFx, is used in W's text and in my comments. P●Q should be read "P and Q." Often the dot is dropped, as in PQ. Occasionally dots are used instead of parentheses.

---

6
The general form of truth-function is: [p‾,ξ‾,N⁡(ξ‾)].

---

See Russell's Introduction for elucidation.

---

This is the general form of proposition.

6.001
This says nothing else than that every proposition is the result of successive applications of the operation N′⁡(ξ‾) to the elementary propositions.

6.002
If we are given the general form of the way in which a proposition is constructed, then thereby we are also given the general form of the way in which by an operation out of one proposition another can be created.

6.01
The general form of the operation Ω′⁡(η‾) is therefore: [ξ‾,N⁡(ξ‾)]′(η‾)(=[η‾,ξ‾,N⁡(ξ‾)]).

This is the most general form of transition from one proposition to another.

6.02
And thus we come to numbers: I define

6.021
A number is the exponent of an operation.

6.022
The concept number is nothing else than that which is common to all numbers, the general form of a number.

The concept number is the variable number.

And the concept of equality of numbers is the general form of all special equalities of numbers.

6.03
The general form of the cardinal number is: [0,ξ,ξ+1].

6.031
The theory of classes is altogether superfluous in mathematics.

---

Sets are not superfluous in formal logic, I maintain, since (x)Fx and (∃x)Fx contain the hidden set X, with x ∈ X. A primitive notion of set is required for the building up of logic. Since mathematics is viewed as dependent on logic, the notion of set must be axiomatic in math. I favor calling the quantifier-related sets ur-sets since no set theory can be constructed without basic logic and the two quantifiers, along with the logic operations of negation, disjunction and conjunction (which can be combined into the single operation nand or not-and).

As Paul Benacerraf and Hilary Putnam say in their Introduction to Philosophy of Mathematics, Selected Readings (Prentice-Hall 1964),

Logicists [in particular Gottlob Frege, Bertrand Russell and A.N. Whitehead] did not reduce all of mathematics to elementary logic, but they did reduce mathematics to elementary logic plus the theory of properties (or sets), properties of properties, properties of properties of properties, and so on. Thus if property theory (or set theory) may be counted as part of logic, mathematics is reducible to logic.

---

This is connected with the fact that the generality which we need in mathematics is not the accidental one.

---

A mathematician would today argue that, given the axioms, a set theory is a form of mathematics. It deals with precise abstract relations, which is what any mathematical area entails.

---

6.1
The propositions of logic are tautologies.

---

I suppose he means by this the axioms.

---

6.11
The propositions of logic therefore say nothing. (They are the analytical propositions.)

6.111
Theories which make a proposition of logic appear substantial are always false. One could e.g. believe that the words “true” and “false” signify two properties among other properties, and then it would appear as a remarkable fact that every proposition possesses one of these properties. This now by no means appears self-evident, no more so than the proposition “All roses are either yellow or red” would seem even if it were true. Indeed our proposition now gets quite the character of a proposition of natural science and this is a certain symptom of its being falsely understood.

6.112
The correct explanation of logical propositions must give them a peculiar position among all propositions.

6.113
It is the characteristic mark of logical propositions that one can perceive in the symbol alone that they are true; and this fact contains in itself the whole philosophy of logic. And so also it is one of the most important facts that the truth or falsehood of non-logical propositions can not be recognized from the propositions alone.

---

This follows from the fact that the symbol, say P, represents a formula (well-formed formula) or relation without specifying the particulars. Thus, P ⊃ P and PQ ⊃ P are viewed as basic laws of thought. One can justify them further (for example, see Rosser, Logic, 1953), but at some point some axioms are "obvious" reflections of proper thought. So P is the symbol for the general formula or general relation. P = aRb means that P_o = aRb. That is, aRb represents an instance of P. aRb may be empirical or it may result from analysis, as in R means "less than." 1R2 is true; 2R1 is false; greenR5 is meaningless.

---

6.12
The fact that the propositions of logic are tautologies shows the formal⁠—logical⁠—properties of language, of the world.

That its constituent parts connected together in this way give a tautology characterizes the logic of its constituent parts.

In order that propositions connected together in a definite way may give a tautology they must have definite properties of structure. That they give a tautology when so connected shows therefore that they possess these properties of structure.

6.1201
That e.g. the propositions “p” and “~p” in the connection “~(p.~p)” give a tautology shows that they contradict one another. That the propositions “p⊃q”, “p” and “q” connected together in the form “(p⊃q).(p):⊃:(q)” give a tautology shows that q follows from p and p⊃q. That “(x).f⁡x:⊃:f⁡a” is a tautology shows that f⁡a follows from (x).f⁡x, etc. etc.

---

One might say that ~(p.~p) is a necessary axiom of logic. It says that contradiction is not permitted. We also need a truth value axiom, I would say, as in: "Any P carries a value of true xor false even if that value can't be determined." Or, "Any P carries a value of T (or 1) xor ~T (or 0) xor U (or undecidable, 2)."^†

---

6.1202
It is clear that we could have used for this purpose contradictions instead of tautologies.

6.1203
In order to recognize a tautology as such, we can, in cases in which no sign of generality occurs in the tautology, make use of the following intuitive method: I write instead of “p”, “q”, “r”, etc., “TpF”, “TqF”, “TrF”, etc. The truth-combinations I express by brackets, e.g.:

The propositions TpF and TqF, connected by brackets above and below. and the coordination of the truth or falsity of the whole proposition with the truth-combinations of the truth-arguments by lines in the following way:

The propositions TpF and TqF, connected by brackets above and below; F is connected from above, and T from below. This sign, for example, would therefore present the proposition p⊃q. Now I will proceed to inquire whether such a proposition as ~(p.~p) (The Law of Contradiction) is a tautology. The form “~ξ” is written in our notation

The proposition T ξ F, with T connected from above and F from below. the form “ξ.η” thus:⁠—

The propositions TξF and TηF, with braces above and below; T is connected from above, and F from below. Hence the proposition ~(p.~q) runs thus:⁠—

The previous three figures merged.
If here we put “p” instead of “q” and examine the combination of the outermost T and F with the innermost, it is seen that the truth of the whole proposition is coordinated with all the truth-combinations of its argument, its falsity with none of the truth-combinations.

6.121
The propositions of logic demonstrate the logical properties of propositions, by combining them into propositions which say nothing.

This method could be called a zero-method. In a logical proposition propositions are brought into equilibrium with one another, and the state of equilibrium then shows how these propositions must be logically constructed.

6.122
Whence it follows that we can get on without logical propositions, for we can recognize in an adequate notation the formal properties of the propositions by mere inspection.

6.1221
If for example two propositions “p” and “q” give a tautology in the connection “p⊃q”, then it is clear that q follows from p.

E.g. that “q” follows from “p⊃q.p” we see from these two propositions themselves, but we can also show it by combining them to “q” follows from “p⊃q.p:⊃:q” and then showing that this is a tautology.

6.1222
This throws light on the question why logical propositions can no more be empirically confirmed than they can be empirically refuted. Not only must a proposition of logic be incapable of being contradicted by any possible experience, but it must also be incapable of being confirmed by any such.

6.1223
It now becomes clear why we often feel as though “logical truths” must be “postulated” by us. We can in fact postulate them in so far as we can postulate an adequate notation.

6.1224
It also becomes clear why logic has been called the theory of forms and of inference.

6.123
It is clear that the laws of logic cannot themselves obey further logical laws.

(There is not, as Russell supposed, for every “type” a special law of contradiction; but one is sufficient, since it is not applied to itself.)

6.1231
The mark of logical propositions is not their general validity.

To be general is only to be accidentally valid for all things. An ungeneralized proposition can be tautologous just as well as a generalized one.

6.1232
Logical general validity, we could call essential as opposed to accidental general validity, e.g. of the proposition “all men are mortal.” Propositions like Russell’s “axiom of reducibility” are not logical propositions, and this explains our feeling that, if true, they can only be true by a happy chance.

6.1233
We can imagine a world in which the axiom of reducibility is not valid. But it is clear that logic has nothing to do with the question whether our world is really of this kind or not.

6.124
The logical propositions describe the scaffolding of the world, or rather they present it. They “treat” of nothing. They presuppose that names have meaning, and that elementary propositions have sense. And this is their connection with the world. It is clear that it must show something about the world that certain combinations of symbols⁠—which essentially have a definite character⁠—are tautologies. Herein lies the decisive point. We said that in the symbols which we use something is arbitrary, something not. In logic only this expresses: but this means that in logic it is not we who express, by means of signs, what we want, but in logic the nature of the essentially necessary signs itself asserts. That is to say, if we know the logical syntax of any sign language, then all the propositions of logic are already given.

6.125
It is possible, also with the old conception of logic, to give at the outset a description of all “true” logical propositions.

6.1251
Hence there can never be surprises in logic.

6.126
Whether a proposition belongs to logic can be calculated by calculating the logical properties of the symbol.

And this we do when we prove a logical proposition. For without troubling ourselves about a sense and a meaning, we form the logical propositions out of others by mere symbolic rules.

We prove a logical proposition by creating it out of other logical propositions by applying in succession certain operations, which again generate tautologies out of the first. (And from a tautology only tautologies follow.)

Naturally this way of showing that its propositions are tautologies is quite unessential to logic. Because the propositions, from which the proof starts, must show without proof that they are tautologies.

6.1261
In logic process and result are equivalent. (Therefore no surprises.)

6.1262
Proof in logic is only a mechanical expedient to facilitate the recognition of tautology, where it is complicated.

6.1263
It would be too remarkable, if one could prove a significant proposition logically from another, and a logical proposition also. It is clear from the beginning that the logical proof of a significant proposition and the proof in logic must be two quite different things.

6.1264
The significant proposition asserts something, and its proof shows that it is so; in logic every proposition is the form of a proof.

Every proposition of logic is a modus ponens presented in signs. (And the modus ponens can not be expressed by a proposition.)

6.1265
Logic can always be conceived to be such that every proposition is its own proof.

6.127
All propositions of logic are of equal rank; there are not some which are essentially primitive and others deduced from there.

Every tautology itself shows that it is a tautology.

6.1271
It is clear that the number of “primitive propositions of logic” is arbitrary, for we could deduce logic from one primitive proposition by simply forming, for example, the logical produce of Frege’s primitive propositions. (Frege would perhaps say that this would no longer be immediately self-evident. But it is remarkable that so exact a thinker as Frege should have appealed to the degree of self-evidence as the criterion of a logical proposition.)

6.13
Logic is not a theory but a reflection of the world.

Logic is transcendental.

6.2
Mathematics is a logical method.

The propositions of mathematics are equations, and therefore pseudo-propositions.

---

In Euclidean geometry, infinitely extended parallel lines never meet. Is this proposition an equation or is the proposition talking about an equality?

---

6.21
Mathematical propositions express no thoughts.

6.211 In life it is never a mathematical proposition which we need, but we use mathematical propositions only in order to infer from propositions which do not belong to mathematics to others which equally do not belong to mathematics.

(In philosophy the question “Why do we really use that word, that proposition?” constantly leads to valuable results.)

6.22
The logic of the world which the propositions of logic show in tautologies, mathematics shows in equations.

6.23
If two expressions are connected by the sign of equality, this means that they can be substituted for one another. But whether this is the case must show itself in the two expressions themselves.

It characterizes the logical form of two expressions, that they can be substituted for one another.

6.231
It is a property of affirmation that it can be conceived as double denial.

It is a property of “1+1+1+1” that it can be conceived as “(1+1)+(1+1)”.

6.232
Frege says that these expressions have the same meaning but different senses.

But what is essential about equation is that it is not necessary in order to show that both expressions, which are connected by the sign of equality, have the same meaning: for this can be perceived from the two expressions themselves.

6.2321
And, that the propositions of mathematics can be proved means nothing else than that their correctness can be seen without our having to compare what they express with the facts as regards correctness.

6.2322
The identity of the meaning of two expressions cannot be asserted. For in order to be able to assert anything about their meaning, I must know their meaning, and if I know their meaning, I know whether they mean the same or something different.

6.2323
The equation characterizes only the standpoint from which I consider the two expressions, that is to say the standpoint of their equality of meaning.

6.233
To the question whether we need intuition for the solution of mathematical problems it must be answered that language itself here supplies the necessary intuition.

6.2331
The process of calculation brings about just this intuition.

Calculation is not an experiment.

6.234
Mathematics is a method of logic.

6.2341
The essential of mathematical method is working with equations. On this method depends the fact that every proposition of mathematics must be self-evident.

6.24
The method by which mathematics arrives at its equations is the method of substitution.

For equations express the substitutability of two expressions, and we proceed from a number of equations to new equations, replacing expressions by others in accordance with the equations.

6.241
Thus the proof of the proposition 2×2=4 runs:

6.3
Logical research means the investigation of all regularity. And outside logic all is accident.

6.31
The so-called law of induction cannot in any case be a logical law, for it is obviously a significant proposition.⁠—And therefore it cannot be a law a priori either.

6.32
The law of causality is not a law but the form of a law.²

6.321
“Law of Causality” is a class name. And as in mechanics there are, for instance, minimum-laws, such as that of least actions, so in physics there are causal laws, laws of the causality form.

6.3211
Men had indeed an idea that there must be a “law of least action,” before they knew exactly how it ran. (Here, as always, the a priori certain proves to be something purely logical.)

6.33
We do not believe a priori in a law of conservation, but we know a priori the possibility of a logical form. 6.34 All propositions, such as the law of causation, the law of continuity in nature, the law of least expenditure in nature, etc. etc., all these are a priori intuitions of possible forms of the propositions of science. 6.341 Newtonian mechanics, for example, brings the description of the universe to a unified form. Let us imagine a white surface with irregular black spots. We now say: Whatever kind of picture these make I can always get as near as I like to its description, if I cover the surface with a sufficiently fine square network and now say of every square that it is white or black. In this way I shall have brought the description of the surface to a unified form. This form is arbitrary, because I could have applied with equal success a net with a triangular or hexagonal mesh. It can happen that the description would have been simpler with the aid of a triangular mesh; that is to say we might have described the surface more accurately with a triangular, and coarser, than with the finer square mesh, or vice versa, and so on. To the different networks correspond different systems of describing the world. Mechanics determine a form of description by saying: All propositions in the description of the world must be obtained in a given way from a number of given propositions⁠—the mechanical axioms. It thus provides the bricks for building the edifice of science, and says: Whatever building thou wouldst erect, thou shalt construct it in some manner with these bricks and these alone.

(As with the system of numbers one must be able to write down any arbitrary number, so with the system of mechanics one must be able to write down any arbitrary physical proposition.)

6.342 And now we see the relative position of logic and mechanics. (We could construct the network out of figures of different kinds, as out of triangles and hexagons together.) That a picture like that instanced above can be described by a network of a given form asserts nothing about the picture. (For this holds of every picture of this kind.) But this does characterize the picture, the fact, namely, that it can be completely described by a definite net of definite fineness.

So too the fact that it can be described by Newtonian mechanics asserts nothing about the world; but this asserts something, namely, that it can be described in that particular way in which as a matter of fact it is described. The fact, too, that it can be described more simply by one system of mechanics than by another says something about the world.

6.343
Mechanics is an attempt to construct according to a single plan all true propositions which we need for the description of the world.

6.3431
Through their whole logical apparatus the physical laws still speak of the objects of the world.

6.3432
We must not forget that the description of the world by mechanics is always quite general. There is, for example, never any mention of particular material points in it, but always only of some points or other.

6.35
Although the spots in our picture are geometrical figures, geometry can obviously say nothing about their actual form and position. But the network is purely geometrical, and all its properties can be given a priori.

Laws, like the law of causation, etc., treat of the network and not what the network describes.

6.36
If there were a law of causality, it might run: “There are natural laws.”

But that can clearly not be said: it shows itself.

6.361
In the terminology of Hertz we might say: Only uniform connections are thinkable.

6.3611
We cannot compare any process with the “passage of time”⁠—there is no such thing⁠—but only with another process (say, with the movement of the chronometer).

Hence the description of the temporal sequence of events is only possible if we support ourselves on another process.

It is exactly analogous for space. When, for example, we say that neither of two events (which mutually exclude one another) can occur, because there is no cause why the one should occur rather than the other, it is really a matter of our being unable to describe one of the two events unless there is some sort of asymmetry. And if there is such an asymmetry, we can regard this as the cause of the occurrence of the one and of the nonoccurrence of the other.

6.36111
The Kantian problem of the right and left hand which cannot be made to cover one another already exists in the plane, and even in one-dimensional space; where the two congruent figures a and b cannot be made to cover one another without

moving them out of this space. The right and left hand are in fact completely congruent. And the fact that they cannot be made to cover one another has nothing to do with it.

A right-hand glove could be put on a left hand if it could be turned round in four-dimensional space.

A right-hand glove could be put on a left hand if it could be turned round in four-dimensional space.

6.362
What can be described can happen too, and what is excluded by the law of causality cannot be described.

6.363
The process of induction is the process of assuming the simplest law that can be made to harmonize with our experience.

6.3631
This process, however, has no logical foundation but only a psychological one. It is clear that there are no grounds for believing that the simplest course of events will really happen.

6.36311
That the sun will rise tomorrow, is an hypothesis; and that means that we do not know whether it will rise.

6.37
A necessity for one thing to happen because another has happened does not exist. There is only logical necessity.

6.371
At the basis of the whole modern view of the world lies the illusion that the so-called laws of nature are the explanations of natural phenomena.

6.372
So people stop short at natural laws as something unassailable, as did the ancients at God and Fate.

And they are both right and wrong. But the ancients were clearer, in so far as they recognized one clear terminus, whereas the modern system makes it appear as though everything were explained.

6.373
The world is independent of my will.

6.374
Even if everything we wished were to happen, this would only be, so to speak, a favour of fate, for there is no logical connection between will and world, which would guarantee this, and the assumed physical connection itself we could not again will.

6.375
As there is only a logical necessity, so there is only a logical impossibility.

6.3751
For two colours, e.g. to be at one place in the visual field, is impossible, logically impossible, for it is excluded by the logical structure of colour.

Let us consider how this contradiction presents itself in physics. Somewhat as follows: That a particle cannot at the same time have two velocities, i.e. that at the same time it cannot be in two places, i.e. that particles in different places at the same time cannot be identical.

It is clear that the logical product of two elementary propositions can neither be a tautology nor a contradiction. The assertion that a point in the visual field has two different colours at the same time, is a contradiction.

6.4
All propositions are of equal value.

6.41
The sense of the world must lie outside the world. In the world everything is as it is and happens as it does happen. In it there is no value⁠—and if there were, it would be of no value.

If there is a value which is of value, it must lie outside all happening and being-so. For all happening and being-so is accidental.

What makes it non-accidental cannot lie in the world, for otherwise this would again be accidental.

It must lie outside the world.

6.42
Hence also there can be no ethical propositions.

Propositions cannot express anything higher.

6.421
It is clear that ethics cannot be expressed.

Ethics is transcendental.

(Ethics and aesthetics are one.)

6.422

The first thought in setting up an ethical law of the form “thou shalt⁠ ⁠…” is: And what if I do not do it? But it is clear that ethics has nothing to do with punishment and reward in the ordinary sense. This question as to the consequences of an action must therefore be irrelevant. At least these consequences will not be events. For there must be something right in that formulation of the question. There must be some sort of ethical reward and ethical punishment, but this must lie in the action itself.

(And this is clear also that the reward must be something acceptable, and the punishment something unacceptable.)

6.423
Of the will as the subject of the ethical we cannot speak.

And the will as a phenomenon is only of interest to psychology.

6.43
If good or bad willing changes the world, it can only change the limits of the world, not the facts; not the things that can be expressed in language.

In brief, the world must thereby become quite another, it must so to speak wax or wane as a whole.

The world of the happy is quite another than that of the unhappy.

6.431
As in death, too, the world does not change, but ceases.

6.4311
Death is not an event of life. Death is not lived through.

If by eternity is understood not endless temporal duration but timelessness, then he lives eternally who lives in the present.

Our life is endless in the way that our visual field is without limit.

6.4312
The temporal immortality of the human soul, that is to say, its eternal survival also after death, is not only in no way guaranteed, but this assumption in the first place will not do for us what we always tried to make it do. Is a riddle solved by the fact that I survive forever? Is this eternal life not as enigmatic as our present one? The solution of the riddle of life in space and time lies outside space and time.

(It is not problems of natural science which have to be solved.)

6.432
How the world is, is completely indifferent for what is higher. God does not reveal himself in the world.

---

He knows this -- how? Divine revelation?

---

6.4321
The facts all belong only to the task and not to its performance.

6.44
Not how the world is, is the mystical, but that it is.

6.45
The contemplation of the world sub specie aeterni is its contemplation as a limited whole.

The feeling that the world is a limited whole is the mystical feeling.

6.5
For an answer which cannot be expressed the question too cannot be expressed.

The riddle does not exist.

If a question can be put at all, then it can also be answered.

6.51
Scepticism is not irrefutable, but palpably senseless, if it would doubt where a question cannot be asked.

For doubt can only exist where there is a question; a question only where there is an answer, and this only where something can be said.

6.52
We feel that even if all possible scientific questions be answered, the problems of life have still not been touched at all. Of course there is then no question left, and just this is the answer.

6.521
The solution of the problem of life is seen in the vanishing of this problem.

(Is not this the reason why men to whom after long doubting the sense of life became clear, could not then say wherein this sense consisted?)

6.522
There is indeed the inexpressible. This shows itself; it is the mystical.

6.53
The right method of philosophy would be this: To say nothing except what can be said, i.e. the propositions of natural science, i.e. something that has nothing to do with philosophy: and then always, when someone else wished to say something metaphysical, to demonstrate to him that he had given no meaning to certain signs in his propositions. This method would be unsatisfying to the other⁠—he would not have the feeling that we were teaching him philosophy⁠—but it would be the only strictly correct method.

6.54
My propositions are elucidatory in this way: he who understands me finally recognizes them as senseless, when he has climbed out through them, on them, over them. (He must so to speak throw away the ladder, after he has climbed up on it.)

He must surmount these propositions; then he sees the world rightly.

---

2. I.e. not the form of one particular law, but of any law of a certain sort. (B. R.)

---

† . T = 1, ~T = 0, U = 2. The rules for 2 are:

2 + 1 = 2
'P is undecidable or true.' P cannot be decided because falsehood is not an option.

2 + 0 = 2
'P is undecidable or false.' P cannot be decided because truth is not an option.

2 + 2 = 2
'P is undecidable or undecidable.' P cannot be decided because it lacks the options of truth and falsehood.

0 + 1 + 2 = 1
'P is false, true or undecidable.' These are all the options; hence P is true.

2*1*0 = 0
'P is undecidable and true and false.' Contradiction,

2*0 = 0
'P is undecidable and false.' Contradiction

2*1 = 0
'P is undecidable and true.' Contradiction.

2*2 = 2
'P is undecidable and undecidable.' A contradiction would make P false, as in 'undecidable and true' or 'undecidable and false.' Thus P is either true or undecidable. But to obtain true, one needs 'true and true.' Hence P is undecidable.

We do not worry about the formulations '0 + 1 = 1' and '0*1 = 0.' That is, though 'undecidable' is not an option, that option may be dropped if there is no reason to call for it.

I concede that this interpretation is debatable.

Tractatus 5

---

When you see X ⊃ Y, you are to read "X implies Y" or "If X, then Y." Sometimes you may see the modern form, X —> Y, in my comments.
When you see X ≡ Y, you should read "X equivalent to Y" or "X strictly implies Y" or "If and only if X, then Y" or "If X, then Y and if Y, then X" (these forms are sometimes shortened to "iff"). "X ≡ Y" can also be read: "Y is necessary for X and X is sufficient for Y." Occasionally one also sees "X ≡ Y" interpreted as "Y holds just in case X holds" or "Y holds only in case X holds" and the converse, "X holds just in case Y holds." Sometimes my comments use the modern X <—> Y.
For the quantifier all, you will see ( ), as in (x)Fx. In my comments I sometimes use the modern symbol ∀, as in ∀xFx. The existential quantifer ∃, as in ∃xFx, is used in W's text and in my comments. P●Q should be read "P and Q." Often the dot is dropped, as in PQ. Occasionally dots are used instead of parentheses.

---

5
Propositions are truth-functions of elementary propositions.

(An elementary proposition is a truth-function of itself.)

5.01
The elementary propositions are the truth-arguments of propositions.

5.02
It is natural to confuse the arguments of functions with the indices of names. For I recognize the meaning of the sign containing it from the argument just as much as from the index.

In Russell’s “+c”, for example, “c” is an index which indicates that the whole sign is the addition sign for cardinal numbers. But this way of symbolizing depends on arbitrary agreement, and one could choose a simple sign instead of “+c”: but in “~p” “p” is not an index but an argument; the sense of “~p” cannot be understood, unless the sense of “p” has previously been understood. (In the name Julius Caesar, Julius is an index. The index is always part of a description of the object to whose name we attach it, e.g. The Caesar of the Julian gens.)

The confusion of argument and index is, if I am not mistaken, at the root of Frege’s theory of the meaning of propositions and functions. For Frege the propositions of logic were names and their arguments the indices of these names.

5.1
The truth-functions can be ordered in series.

That is the foundation of the theory of probability.

5.101
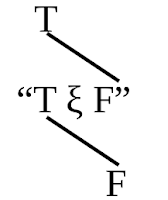
The truth-functions of every number of elementary propositions can be written in a schema of the following kind:

Those truth-possibilities of its truth-arguments, which verify the proposition, I shall call its truth-grounds.

5.11
If the truth-grounds which are common to a number of propositions are all also truth-grounds of some one proposition, we say that the truth of this proposition follows from the truth of those propositions.

5.12
In particular the truth of a proposition p follows from that of a proposition q, if all the truth-grounds of the second are truth-grounds of the first.

5.121
The truth-grounds of q are contained in those of p; p follows from q.

5.122
If p follows from q, the sense of “p” is contained in that of “q”.

5.123
If a god creates a world in which certain propositions are true, he creates thereby also a world in which all propositions consequent on them are true. And similarly he could not create a world in which the proposition “p” is true without creating all its objects.

5.124
A proposition asserts every proposition which follows from it.

5.1241

“p.q” is one of the propositions which assert “p” and at the same time one of the propositions which assert “q”.

Two propositions are opposed to one another if there is no significant proposition which asserts them both.

Every proposition which contradicts another, denies it.

5.13
That the truth of one proposition follows from the truth of other propositions, we perceive from the structure of the propositions.

5.131
If the truth of one proposition follows from the truth of others, this expresses itself in relations in which the forms of these propositions stand to one another, and we do not need to put them in these relations first by connecting them with one another in a proposition; for these relations are internal, and exist as soon as, and by the very fact that, the propositions exist.

5.1311
When we conclude from p∨q and ~p to q the relation between the forms of the propositions “p∨q” and “~p” is here concealed by the method of symbolizing. But if we write, e.g. instead of “p∨q” “p|q.|.p|q” and instead of “~p” “p|p” (p|q = neither p nor q), then the inner connection becomes obvious.

(The fact that we can infer f⁡a from (x).f⁡x shows that generality is present also in the symbol “(x).f⁡x”.

5.132
If p follows from q, I can conclude from q to p; infer p from q.

The method of inference is to be understood from the two propositions alone.

Only they themselves can justify the inference.

Laws of inference, which⁠—as in Frege and Russell⁠—are to justify the conclusions, are senseless and would be superfluous.

5.133
All inference takes place a priori.

5.134
From an elementary proposition no other can be inferred.

5.135
In no way can an inference be made from the existence of one state of affairs to the existence of another entirely different from it.

5.136
There is no causal nexus which justifies such an inference.

5.1361
The events of the future cannot be inferred from those of the present.

Superstition is the belief in the causal nexus.

5.1362
The freedom of the will consists in the fact that future actions cannot be known now. We could only know them if causality were an inner necessity, like that of logical deduction.⁠—The connection of knowledge and what is known is that of logical necessity.

(“A knows that p is the case” is senseless if p is a tautology.)

5.1363
If from the fact that a proposition is obvious to us it does not follow that it is true, then obviousness is no justification for our belief in its truth.

5.14
If a proposition follows from another, then the latter says more than the former, the former less than the latter.

5.141
If p follows from q and q from p then they are one and the same proposition.

5.142
A tautology follows from all propositions: it says nothing.

5.143
Contradiction is something shared by propositions, which no proposition has in common with another. Tautology is that which is shared by all propositions, which have nothing in common with one another.

Contradiction vanishes so to speak outside, tautology inside all propositions.

Contradiction is the external limit of the propositions, tautology their substanceless centre.

5.15
If Tr is the number of the truth-grounds of the proposition “r”, Trs the number of those truth-grounds of the proposition “s” which are at the same time truth-grounds of “r”, then we call the ratio Trs:Tr the measure of the probability which the proposition “r” gives to the proposition “s”.

5.151
Suppose in a schema like that above in No. 5.101 Tr is the number of the “T”’s in the proposition r, Trs the number of those “T”’s in the proposition s, which stand in the same columns as “T”’s of the proposition r; then the proposition r gives to the proposition s the probability Trs:Tr.

5.1511
There is no special object peculiar to probability propositions.

5.152
Propositions which have no truth-arguments in common with each other we call independent.

Independent propositions (e.g. any two elementary propositions) give to one another the probability ½.

If p follows from q, the proposition q gives to the proposition p the probability 1. The certainty of logical conclusion is a limiting case of probability.

(Application to tautology and contradiction.)

5.153
A proposition is in itself neither probable nor improbable. An event occurs or does not occur, there is no middle course.

5.154
In an urn there are equal numbers of white and black balls (and no others). I draw one ball after another and put them back in the urn. Then I can determine by the experiment that the numbers of the black and white balls which are drawn approximate as the drawing continues.

So this is not a mathematical fact.

If then, I say, It is equally probable that I should draw a white and a black ball, this means, All the circumstances known to me (including the natural laws hypothetically assumed) give to the occurrence of the one event no more probability than to the occurrence of the other. That is they give⁠—as can easily be understood from the above explanations⁠—to each the probability ½.

What I can verify by the experiment is that the occurrence of the two events is independent of the circumstances with which I have no closer acquaintance.

5.155
The unit of the probability proposition is: The circumstances⁠—with which I am not further acquainted⁠—give to the occurrence of a definite event such and such a degree of probability.

5.156
Probability is a generalization.

It involves a general description of a propositional form.

Only in default of certainty do we need probability. If we are not completely acquainted with a fact, but know something about its form.

(A proposition can, indeed, be an incomplete picture of a certain state of affairs, but it is always a complete picture.)

The probability proposition is, as it were, an extract from other propositions.

5.2
The structures of propositions stand to one another in internal relations.

5.21
We can bring out these internal relations in our manner of expression, by presenting a proposition as the result of an operation which produces it from other propositions (the bases of the operation).

5.22
The operation is the expression of a relation between the structures of its result and its bases.

5.23
The operation is that which must happen to a proposition in order to make another out of it.

5.231
And that will naturally depend on their formal properties, on the internal similarity of their forms.

5.232
The internal relation which orders a series is equivalent to the operation by which one term arises from another.

5.233
The first place in which an operation can occur is where a proposition arises from another in a logically significant way; i.e. where the logical construction of the proposition begins.

5.234
The truth-functions of elementary proposition, are results of operations which have the elementary propositions as bases. (I call these operations, truth-operations.)

5.2341
The sense of a truth-function of p is a function of the sense of p.

Denial, logical addition, logical multiplication, etc., etc., are operations.

(Denial reverses the sense of a proposition.)

5.24
An operation shows itself in a variable; it shows how we can proceed from one form of proposition to another.

It gives expression to the difference between the forms.

(And that which is common to the bases, and the result of an operation, is the bases themselves.)

5.241
The operation does not characterize a form but only the difference between forms.

5.242
The same operation which makes “q” from “p”, makes “r” from “q”, and so on. This can only be expressed by the fact that “p”, “q”, “r”, etc., are variables which give general expression to certain formal relations.

5.25
The occurrence of an operation does not characterize the sense of a proposition.

For an operation does not assert anything; only its result does, and this depends on the bases of the operation.

(Operation and function must not be confused with one another.)

5.251 A function cannot be its own argument, but the result of an operation can be its own basis.

5.252
Only in this way is the progress from term to term in a formal series possible (from type to type in the hierarchy of Russell and Whitehead). (Russell and Whitehead have not admitted the possibility of this progress but have made use of it all the same.)

5.2521
The repeated application of an operation to its own result I call its successive application (“O′⁡O′⁡O′⁡a” is the result of the threefold successive application of “O′ξ” to “a”).

In a similar sense I speak of the successive application of several operations to a number of propositions.

5.2522
The general term of the formal series a, O′⁡a, O′⁡O′⁡a,⁠ ⁠… I write thus: “[a,x,O′⁡x]”. This expression in brackets is a variable. The first term of the expression is the beginning of the formal series, the second the form of an arbitrary term x of the series, and the third the form of that term of the series which immediately follows x.

5.2523
The concept of the successive application of an operation is equivalent to the concept “and so on.”

5.253
One operation can reverse the effect of another. Operations can cancel one another.

5.254
Operations can vanish (e.g. denial in “~~p”. ~~p=p).

5.3 All propositions are results of truth-operations on the elementary propositions.

The truth-operation is the way in which a truth-function arises from elementary propositions.

According to the nature of truth-operations, in the same way as out of elementary propositions arise their truth-functions, from truth-functions arises a new one. Every truth-operation creates from truth-functions of elementary propositions, another truth-function of elementary propositions i.e. a proposition. The result of every truth-operation on the results of truth-operations on elementary propositions is also the result of one truth-operation on elementary propositions.

Every proposition is the result of truth-operations on elementary propositions.

5.31
The schemata No. 4.31 are also significant, if “p”, “q”, “r”, etc. are not elementary propositions.

And it is easy to see that the propositional sign in No. 4.442 expresses one truth-function of elementary propositions even when “p” and “q” are truth-functions of elementary propositions.

5.32
All truth-functions are results of the successive application of a finite number of truth-operations to elementary propositions.

5.4

Here it becomes clear that there are no such things as “logical objects” or “logical constants” (in the sense of Frege and Russell).

5.41
For all those results of truth-operations on truth-functions are identical, which are one and the same truth-function of elementary propositions.

5.42
That ∨, ⊃, etc., are not relations in the sense of right and left, etc., is obvious.

The possibility of crosswise definition of the logical “primitive signs” of Frege and Russell shows by itself that these are not primitive signs and that they signify no relations.

And it is obvious that the “⊃” which we define by means of “~” and “∨” is identical with that by which we define “∨” with the help of “~”, and that this “∨” is the same as the first, and so on.

5.43
That from a fact p an infinite number of others should follow, namely, ~~p, ~~~~p, etc., is indeed hardly to be believed, and it is no less wonderful that the infinite number of propositions of logic (of mathematics) should follow from half a dozen “primitive propositions.”

But the propositions of logic say the same thing. That is, nothing.

5.44
Truth-functions are not material functions.

If e.g. an affirmation can be produced by repeated denial, is the denial⁠—in any sense⁠—contained in the affirmation? Does “~~p” deny ~p, or does it affirm p; or both?

The proposition “~~p” does not treat of denial as an object, but the possibility of denial is already prejudged in affirmation.

And if there was an object called “~”, then “~~p” would have to say something other than “p”. For the one proposition would then treat of ~, the other would not.

5.441
This disappearance of the apparent logical constants also occurs if “~(∃x).~f⁡x” says the same as “(x).f⁡x”, or “(∃x).f⁡x.x=a” the same as “f⁡a”.

5.442
If a proposition is given to us then the results of all truth-operations which have it as their basis are given with it.

5.45
If there are logical primitive signs a correct logic must make clear their position relative to one another and justify their existence. The construction of logic out of its primitive signs must become clear.

5.451
If logic has primitive ideas these must be independent of one another. If a primitive idea is introduced it must be introduced in all contexts in which it occurs at all. One cannot therefore introduce it for one context and then again for another. For example, if denial is introduced, we must understand it in propositions of the form “~p”, just as in propositions like “~(p∨q)”, “(∃x).~f⁡x” and others. We may not first introduce it for one class of cases and then for another, for it would then remain doubtful whether its meaning in the two cases was the same, and there would be no reason to use the same way of symbolizing in the two cases.

(In short, what Frege (Grundgesetze der Arithmetik) has said about the introduction of signs by definitions holds, mutatis mutandis, for the introduction of primitive signs also.)

5.452
The introduction of a new expedient in the symbolism of logic must always be an event full of consequences. No new symbol may be introduced in logic in brackets or in the margin⁠—with, so to speak, an entirely innocent face.

(Thus in the Principia Mathematica of Russell and Whitehead there occur definitions and primitive propositions in words. Why suddenly words here? This would need a justification. There was none, and can be none for the process is actually not allowed.)

But if the introduction of a new expedient has proved necessary in one place, we must immediately ask: Where is this expedient always to be used? Its position in logic must be made clear.

5.453
All numbers in logic must be capable of justification.

Or rather it must become plain that there are no numbers in logic.

There are no preeminent numbers.

5.454
In logic there is no side by side, there can be no classification.

In logic there cannot be a more general and a more special.

5.4541
The solution of logical problems must be neat for they set the standard of neatness.

Men have always thought that there must be a sphere of questions whose answers⁠—a priori⁠—are symmetrical and united into a closed regular structure.

A sphere in which the proposition, simplex sigillum veri, is valid.

5.46
When we have rightly introduced the logical signs, the sense of all their combinations has been already introduced with them: therefore not only “p∨q” but also “~(p∨~q)”, etc. etc. We should then already have introduced the effect of all possible combinations of brackets; and it would then have become clear that the proper general primitive signs are not “p∨q”, “(∃x).f⁡x”, etc., but the most general form of their combinations.

5.461
The apparently unimportant fact that the apparent relations like ∨ and ⊃ need brackets⁠—unlike real relations⁠—is of great importance.

The use of brackets with these apparent primitive signs shows that these are not the real primitive signs; and nobody of course would believe that the brackets have meaning by themselves.

5.4611
Logical operation signs are punctuations.

5.47
It is clear that everything which can be said beforehand about the form of all propositions at all can be said on one occasion.

For all logical operations are already contained in the elementary proposition. For “f⁡a” says the same as “(∃x).f⁡x.x=a”.

Where there is composition, there is argument and function, and where these are, all logical constants already are.

One could say: the one logical constant is that which all propositions, according to their nature, have in common with one another.

That however is the general form of proposition.

5.471
The general form of proposition is the essence of proposition.

5.4711
To give the essence of proposition means to give the essence of all description, therefore the essence of the world.

5.472
The description of the most general propositional form is the description of the one and only general primitive sign in logic.

5.473
Logic must take care of itself.

A possible sign must also be able to signify. Everything which is possible in logic is also permitted. (“Socrates is identical” means nothing because there is no property which is called “identical.” The proposition is senseless because we have not made some arbitrary determination, not because the symbol is in itself unpermissible.)

In a certain sense we cannot make mistakes in logic.

5.4731
Self-evidence, of which Russell has said so much, can only be discard in logic by language itself preventing every logical mistake. That logic is a priori consists in the fact that we cannot think illogically.

5.4732
We cannot give a sign the wrong sense.

5.47321
Occam’s razor is, of course, not an arbitrary rule nor one justified by its practical success. It simply says that unnecessary elements in a symbolism mean nothing.

Signs which serve one purpose are logically equivalent, signs which serve no purpose are logically meaningless.

5.4733
Frege says: Every legitimately constructed proposition must have a sense; and I say: Every possible proposition is legitimately constructed, and if it has no sense this can only be because we have given no meaning to some of its constituent parts.

(Even if we believe that we have done so.)

Thus “Socrates is identical” says nothing, because we have given no meaning to the word “identical” as adjective. For when it occurs as the sign of equality it symbolizes in an entirely different way⁠—the symbolizing relation is another⁠—therefore the symbol is in the two cases entirely different; the two symbols have the sign in common with one another only by accident.

5.474
The number of necessary fundamental operations depends only on our notation.

5.475
It is only a question of constructing a system of signs of a definite number of dimensions⁠—of a definite mathematical multiplicity.

5.476
It is clear that we are not concerned here with a number of primitive ideas which must be signified but with the expression of a rule.

5.5
Every truth-function is a result of the successive application of the operation (−−−−−T)(ξ,.....) to elementary propositions.

This operation denies all the propositions in the right-hand bracket and I call it the negation of these propositions.

5.501
An expression in brackets whose terms are propositions I indicate⁠—if the order of the terms in the bracket is indifferent⁠—by a sign of the form “(ξ‾)”. “ξ” is a variable whose values are the terms of the expression in brackets, and the line over the variable indicates that it stands for all its values in the bracket.

(Thus if ξ has the 3 values P, Q, R, then (ξ‾)=(PQR).)

The values of the variables must be determined.

The determination is the description of the propositions which the variable stands for.

How the description of the terms of the expression in brackets takes place is unessential.

We may distinguish 3 kinds of description: 1. Direct enumeration. In this case we can place simply its constant values instead of the variable. 2. Giving a function f⁡x, whose values for all values of x are the propositions to be described. 3. Giving a formal law, according to which those propositions are constructed. In this case the terms of the expression in brackets are all the terms of a formal series.

5.502
Therefore I write instead of “(−−−−−T)(ξ,.....)”, “N⁡(ξ‾)”.

N⁡(ξ‾) is the negation of all the values of the propositional variable ξ.

5.503
As it is obviously easy to express how propositions can be constructed by means of this operation and how propositions are not to be constructed by means of it, this must be capable of exact expression.

5.51
If ξ has only one value, then N⁡(ξ‾)=~p (not p), if it has two values then N⁡(ξ‾)=~p.~q (neither p nor q).

5.511
How can the all-embracing logic which mirrors the world use such special catches and manipulations? Only because all these are connected into an infinitely fine network, to the great mirror.

5.512
“~p” is true if “p” is false. Therefore in the true proposition “~p” “p” is a false proposition. How then can the stroke “~” bring it into agreement with reality?

That which denies in “~p” is however not “~”, but that which all signs of this notation, which deny p, have in common.

Hence the common rule according to which “~p”, “~~~p”, “~p∨~p”, “~p.~p”, etc. etc. (to infinity) are constructed. And this which is common to them all mirrors denial.

5.513
We could say: What is common to all symbols, which assert both p and q, is the proposition “p.q”. What is common to all symbols, which asserts either p or q, is the proposition “p∨q”.

And similarly we can say: Two propositions are opposed to one another when they have nothing in common with one another; and every proposition has only one negative, because there is only one proposition which lies altogether outside it.

Thus in Russell’s notation also it appears evident that “q:p∨~p” says the same thing as “q”; that “p∨~p” says nothing.

5.514
If a notation is fixed, there is in it a rule according to which all the propositions denying p are constructed, a rule according to which all the propositions asserting p are constructed, a rule according to which all the propositions asserting p or q are constructed, and so on. These rules are equivalent to the symbols and in them their sense is mirrored.

5.515
It must be recognized in our symbols that what is connected by “∨”, “.”, etc., must be propositions.

And this is the case, for the symbols “p” and “q” assume “∨”, “~”, etc. If the sign “p” in “p∨q” does not stand for a complex sign, then by itself it cannot have sense; but then also the signs “p∨p”, “p.p”, etc. which have the same sense as “p” have no sense. If, however, “p∨p” has no sense, then also “p∨q” can have no sense.

5.5151
Must the sign of the negative proposition be constructed by means of the sign of the positive? one not be able to express the negative proposition by means of a negative fact? (Like: if “a” does not stand in a certain relation to “b”, it could express that aRb is not the case.)

But here also the negative proposition is indirectly constructed with the positive.

The positive proposition must presuppose the existence of the negative proposition and conversely.

5.52
If the values of ξ are the total values of a function f⁡x for all values of x, then N⁡(ξ‾)=~(∃x).f⁡x.

5.521
I separate the concept all from the truth-function.

Frege and Russell have introduced generality in connection with the logical product or the logical sum. Then it would be difficult to understand the propositions “(∃x).f⁡x” and “(x).f⁡x” in which both ideas lie concealed.

Not to quibble, but Aristotle introduced the all and some quantifiers into logic.

We may regard the a,e,i,o syllogisms using modern set notation.

a)  A = {b|b is x}. All is understood.
i)    A ∩ {b|b is x} ≠ ∅. Some is implied.
e)  A ∩ {b|b is x} = ∅. All is implied.
o)  A ∩ {b|b is not x} ≠ ∅. Some is implied.

As to making the quantifier distinct from the truth function, this act assists us when discussing the subject. But one may argue that symbolic logic uses modus ponens or equivalent and that that operation is essentially syllogistic. That is, some sort of primeval, at least, sets are implied. The function Fx says that the formula F holds true for x. We do not know here whether x ∈ X = {x}, a singleton, or whether X is non-singleton. But, either way, the lack of a quantifier implies the quantifier all. That is, the set X is implied as defined as the applicable x or x's. And, it is also correct to infer that when some x in X is plugged into F, that that holds. I.e., All implies Some.

There really is no need for an all quantifier. The some quantifier is useful for the possibility of not all and not none. But, I don't advocate dispensing with the all quantifier as it makes life easier for the reader.

5.522
That which is peculiar to the “symbolism of generality” is firstly, that it refers to a logical prototype, and secondly, that it makes constants prominent.

5.523
The generality symbol occurs as an argument.

5.524
If the objects are given, therewith are all objects also given.

If the elementary propositions are given, then therewith all elementary propositions are also given.

5.525
It is not correct to render the proposition “(∃x).f⁡x”⁠—as Russell does⁠—in the words “f⁡x is possible.”

Certainty, possibility or impossibility of a state of affairs are not expressed by a proposition but by the fact that an expression is a tautology, a significant proposition or a contradiction.

That precedent to which one would always appeal, must be present in the symbol itself.

---

I am uncertain as to the value of this hair-splitting. Perhaps the problem is that W. was thinking in German, though of course he spoke English with high fluency. That is, “(∃x).f⁡x” means that for at least one x, f holds true. So one is justified in saying "f is possible" or "fx is possible." I think W. was interpreting the word possible in a sense in which reality, as he understood it, is never possible, but just is. But here possible is akin to the word probable. That is, the information yields something less than certainty and more than impossibility.

Also of interest here is the idea of contingency. We usually read

"P → Q" as "If P, then Q."

We are not automatically certifying the truth of P. So (∃x).f⁡x means that f holds for some case x, or, x_i → f. I understand that when I do this I am mixing symbolism apples and oranges. Yet, it seems that the two expressions are interrelated.

---

5.526
One can describe the world completely by completely generalized propositions, i.e. without from the outset coordinating any name with a definite object.

In order then to arrive at the customary way of expression we need simply say after an expression “there is one and only one x, which⁠ ⁠…”: and this x is a.

5.5261
A completely generalized proposition is like every other proposition composite. (This is shown by the fact that in “(∃x,φ).φx” we must mention “φ” and “x” separately. Both stand independently in signifying relations to the world as in the ungeneralized proposition.)

A characteristic of a composite symbol: it has something in common with other symbols.

5.5262
The truth or falsehood of every proposition alters something in the general structure of the world. And the range which is allowed to its structure by the totality of elementary propositions is exactly that which the completely general propositions delimit.

(If an elementary proposition is true, then, at any rate, there is one more elementary proposition true.)

5.53
Identity of the object I express by identity of the sign and not by means of a sign of identity. Difference of the objects by difference of the signs.

5.5301
That identity is not a relation between objects is obvious. This becomes very clear if, for example, one considers the proposition “(x):f⁡x.⊃.x=a”. What this proposition says is simply that only a satisfies the function f, and not that only such things satisfy the function f which have a certain relation to a.

One could of course say that in fact only a has this relation to a, but in order to express this we should need the sign of identity itself.

5.5302
Russell’s definition of “=” won’t do; because according to it one cannot say that two objects have all their properties in common. (Even if this proposition is never true, it is nevertheless significant.)

---

Here is where modern information theory comes in handy. We may regard equality to mean that two signals carry x percent of information in common. Of course, that amounts to saying that X ∩ Y ⊃ X = Y if X and Y have a certain percentage of elements in common.

Of course, in mathematics the percentage is 100. But in the "real world," 100 percent is an unrealistic expectation. In fact, our naming convention in human language is to call things "the same" when they share only a percentage of properties in common.

Shannon information does not suit the word equivalence quite so well. Equivalence has more to do with process than with thing, though in math the two concepts overlap. I think the standard logical definition of equivalence "X ⊃ Y and Y ⊃ X" is a good one for general purposes.

Russell's definition of identity, by the way, has been subjected to challenge. He requires Leibnizian indiscernables as a means of justifying his axiom of reducibility, which he found necessary for his theory of types brought out in Principia Mathematica. As Russell notes in the introduction, W has undermined that notion on logical grounds. It must be granted that Russell was never comfortable with the reducibility axiom.

---

5.5303
Roughly speaking: to say of two things that they are identical is nonsense, and to say of one thing that it is identical with itself is to say nothing.

---

Self-identity adds no information as to the object at hand. But why do mathematicians think well of it? Consistency and completeness have something to do with that preference, I suppose. And one can, for example, imagine "a = a" as part of a reductio ad absurdum argument. "Suppose P. In that case Q, which would mean a =/= a."

---

5.531
I write therefore not “f⁡(a,b).a=b” but “f⁡(aa)” (or “f⁡(bb)”). And not “f⁡(a,b).~a=b”, but “f⁡(a,b)”.

5.532
And analogously: not “(∃x,y).f⁡(x,y).x=y”, but “(∃x).f⁡(x,x)”; and not “(∃x,y).f⁡(x,y).~x=y”, but “(∃x,y).f⁡(x,y)”.

(Therefore instead of Russell’s “(∃x,y).f⁡(x,y)”: “(∃x,y).f⁡(x,y).∨.(∃x).f⁡(x,x)”.)

5.5321
Instead of “(x):f⁡x⊃x=a” we therefore write e.g. “(∃x).f⁡x.⊃.f⁡a:~(∃x,y).f⁡x.f⁡y”.

And if the proposition “only one x satisfies f⁡()” reads: “(∃x).f⁡x:~(∃x,y).f⁡x.f⁡y”.

5.533
The identity sign is therefore not an essential constituent of logical notation.

5.534
And we see that the apparent propositions like: “a=a”, “a=b.b=c.⊃a=c”, “(x).x=x”. “(∃x).x=a”, etc. cannot be written in a correct logical notation at all.

5.535
So all problems disappear which are connected with such pseudo-propositions.

This is the place to solve all the problems with arise through Russell’s “Axiom of Infinity.”

What the axiom of infinity is meant to say would be expressed in language by the fact that there is an infinite number of names with different meanings.

5.5351
There are certain cases in which one is tempted to use expressions of the form “a = a” or “p ⊃ p”. As, for instance, when one would speak of the archetype Proposition, Thing, etc. So Russell in the Principles of Mathematics has rendered the nonsense “p is a proposition” in symbols by “p ⊃ p” and has put it as hypothesis before certain propositions to show that their places for arguments could only be occupied by propositions.

(It is nonsense to place the hypothesis p ⊃ p before a proposition in order to ensure that its arguments have the right form, because the hypotheses for a non-proposition as argument becomes not false but meaningless, and because the proposition itself becomes senseless for arguments of the wrong kind, and therefore it survives the wrong arguments no better and no worse than the senseless hypothesis attached for this purpose.)

---

W appears to have put his finger on an error in Russell's 1903 book, but W's analysis is open to question. Plainly, "p is a proposition" ought have the representation P or R or A. But I suppose we must be talking about self-referencing, as in "This sentence is this sentence." Because a sentence is a relation of the form

IS< this sentence, this sentence >, or I< s,s >

we think it odd, though not altogether illogical.

In any case, a number of logicians have felt it necessary to justify the general tautologies "a = a" and “p ⊃ p” in order to make sure their particular axioms work out (see, for example, Logic for Mathematicians by J. Barkley Rosser, McGraw-Hill 1953¹.)

---

5.5352
Similarly it was proposed to express “There are no things” by “~(∃x).x=x”. But even if this were a proposition⁠—would it not be true if indeed “There were things,” but these were not identical with themselves?

---

W does believes it senseless to speak of a general thing. He says it is incorrect to speak of "100 things." Well, I have no problem with speaking of a pure abstraction. It is like speaking of A ∩ B = ∅. The null set is what's left after you abstract sets away. It's not really a set, but we'll take it because of its utility.

Also, these days we know that when we write ∃x, we mean (∃x ∈ X) and likewise for ∀x, we imply (∀x ∈ X). But this would not have been acceptable to Russell, who with Whitehead, attempted to derive sets from symbolic logic. So to say "~(∃x).x=x" is acceptable if we have some definition of X. Still, if we wanted to symbolize the idea of absolute nothing, why should we not use "~(∃x).x=x"?

Well, since absolute nothing is represented by the concept absolute nothing, we must call absolute nothing a thing. Hence one of the x's -- we'll dub it x_o -- must represent it. Then we have ~(∃x).x=x ⊃ x_o, which means ~(∃x).x=x ⊃ (∃x).x=x, a contradiction.

So we must adopt an axiom that results in the ultimate abstraction -- in this case, absolute nothing -- not being one of the x's. That is, we must say that an empty universe is not a thing.

The self-referencing issue of course brings into play the notion of types and the similar notion of stages of construction of sets. Let us say that we have at hand some thing. We cannot refer to it or point to it unless we give it a name. k is the name we choose. That is, k is a symbol used to represent a primitive concept, or thing.

But in that case, we have that "k represents some thing" is itself a concept, which we name k'. From the base case, we get lim_n-->∞ k⁽ⁿ⁾. That is, put in terms of relations, we have lim_n-->∞ k⁽ⁿ⁺¹⁾Rkⁿ.

In fact, we have stumbled upon F.H. Bradley's point about relations hinging on infinities.

Now PM's axiom of reducibility, if I follow it, says that P⁽ⁿ⁺¹⁾ ⊃ P⁽ⁿ⁾, where P is a proposition. That would then say that any P⁽ⁿ⁾ ⊃ P⁰. [The axiom is discussed further in the footnote ‡ .]

Is this reasonable? Let's look at a proposition as a relation with a truth value. 'P⁽⁰⁾' means here 'k represents a thing', or 'kR[ur]'. Here [ur] means an object prior to naming or description.

kR[ur] must be a tautology, as [ur] is nothing special before being identified/named. In fact let us say that k⁽⁰⁾ is defined as [ur]. Any name j represents [ur]. That is, j⁽⁰⁾ ≡_df [ur]. That is, k⁽¹⁾R k⁽⁰⁾ is a tautology. So the reducibility axiom holds in this base case. In fact, it does seem that k⁽ⁿ⁺¹⁾R k⁽ⁿ⁾ is reasonable since our notation reflects how the naming process works. But we have not demonstrated that any proposition P⁽ⁿ⁺¹⁾ ⊃ Pⁿ.

We can identify with W's claim that a bare object or thing cannot exist, as it must be defined. The [ur] concept is not meant to claim that the objects of perception are all fundamentally identical. Rather, we use [ur] as a general form for any primitive, pre-defined thing.

Also, note that the above axiom itself is a proposition; call it Q. Would this mean Q⁽ⁿ⁺¹⁾ ⊃ Qⁿ ? Would we have an infinity of such axioms?

Such issues tell us why the axiom of reducibility never caught on.

---

5.54
In the general propositional form, propositions occur in a proposition only as bases of the truth-operations.

5.541
At first sight it appears as if there were also a different way in which one proposition could occur in another.

Especially in certain propositional forms of psychology, like “A thinks, that p is the case,” or “A thinks p”, etc.

Here it appears superficially as if the proposition p stood to the object A in a kind of relation.

(And in modern epistemology (Russell, Moore, etc.) those propositions have been conceived in this way.)

5.542
But it is clear that “A believes that p,” “A thinks p,” “A says p,” are of the form “ ‘p’ says p”: and here we have no coordination of a fact and an object, but a coordination of facts by means of a coordination of their objects.

5.5421
This shows that there is no such thing as the soul⁠—the subject, etc.⁠—as it is conceived in superficial psychology. A composite soul would not be a soul any longer.

5.5422
The correct explanation of the form of the proposition “A judges p” must show that it is impossible to judge a nonsense. (Russell’s theory does not satisfy this condition.)

5.5423
To perceive a complex means to perceive that its constituents are combined in such and such a way.

This perhaps explains that the figure

can be seen in two ways as a cube; and all similar phenomena. For we really see two different facts.

(If I fix my eyes first on the corners a and only glance at b, a appears in front and b behind, and vice versa.)

5.55
We must now answer a priori the question as to all possible forms of the elementary propositions. The elementary proposition consists of names. Since we cannot give the number of names with different meanings, we cannot give the composition of the elementary proposition.

5.551
Our fundamental principle is that every question which can be decided at all by logic can be decided offhand. (And if we get into a situation where we need to answer such a problem by looking at the world, this shows that we are on a fundamentally wrong track.)

5.552
The “experience” which we need to understand logic is not that such and such is the case, but that something is; but that is no experience.

Logic precedes every experience⁠—that something is so.

It is before the How, not before the What.

5.5521
And if this were not the case, how could we apply logic? We could say: if there were a logic, even if there were no world, how then could there be a logic, since there is a world?

5.553 Russell said that there were simple relations between different numbers of things (individuals). But between what numbers? And how should this be decided⁠—by experience?

(There is no preeminent number.)

5.554
The enumeration of any special forms would be entirely arbitrary.

5.5541
How could we decide a priori whether, for example, I can get into a situation in which I need to symbolize with a sign of a 27-termed relation?

5.5542
May we then ask this at all? Can we set out a sign form and not know whether anything can correspond to it?

Has the question sense: what must there be in order that anything can be the case?

5.555
It is clear that we have a concept of the elementary proposition apart from its special logical form.

Where, however, we can build symbols according to a system, there this system is the logically important thing and not the single symbols.

And how would it be possible that I should have to deal with forms in logic which I can invent: but I must have to deal with that which makes it possible for me to invent them.

5.556
There cannot be a hierarchy of the forms of the elementary propositions. Only that which we ourselves construct can we foresee.

5.5561
Empirical reality is limited by the totality of objects. The boundary appears again in the totality of elementary propositions.

The hierarchies are and must be independent of reality.

5.5562
If we know on purely logical grounds, that there must be elementary propositions, then this must be known by everyone who understands propositions in their unanalysed form.

5.5563
All propositions of our colloquial language are actually, just as they are, logically completely in order. That simple thing which we ought to give here is not a model of the truth but the complete truth itself.

(Our problems are not abstract but perhaps the most concrete that there are.)

5.557
The application of logic decides what elementary propositions there are.

What lies in its application logic cannot anticipate.

It is clear that logic may not conflict with its application.

But logic must have contact with its application.

Therefore logic and its application may not overlap each other.

5.5571
If I cannot give elementary propositions a priori then it must lead to obvious nonsense to try to give them.

5.6
The limits of my language mean the limits of my world.

5.61
Logic fills the world: the limits of the world are also its limits.

We cannot therefore say in logic: This and this there is in the world, that there is not.

For that would apparently presuppose that we exclude certain possibilities, and this cannot be the case since otherwise logic must get outside the limits of the world: that is, if it could consider these limits from the other side also.

What we cannot think, that we cannot think: we cannot therefore say what we cannot think.

5.62
This remark provides a key to the question, to what extent solipsism is a truth.

In fact what solipsism means, is quite correct, only it cannot be said, but it shows itself.

That the world is my world, shows itself in the fact that the limits of the language (the language which I understand) mean the limits of my world.

5.621
The world and life are one.

5.63
I am my world. (The microcosm.)

5.631
The thinking, presenting subject; there is no such thing.

If I wrote a book “The world as I found it,” I should also have therein to report on my body and say which members obey my will and which do not, etc. This then would be a method of isolating the subject or rather of showing that in an important sense there is no subject: that is to say, of it alone in this book mention could not be made.

5.632
The subject does not belong to the world but it is a limit of the world.

5.633
Where in the world is a metaphysical subject to be noted?

You say that this case is altogether like that of the eye and the field of sight. But you do not really see the eye.

And from nothing in the field of sight can it be concluded that it is seen from an eye.

5.6331
For the field of sight has not a form like this:

5.634
This is connected with the fact that no part of our experience is also a priori.

Everything we see could also be otherwise.

Everything we describe at all could also be otherwise.

There is no order of things a priori.

5.64
Here we see that solipsism strictly carried out coincides with pure realism. The I in solipsism shrinks to an extensionless point and there remains the reality coordinated with it.

5.641
There is therefore really a sense in which the philosophy we can talk of a non-psychological I.

The I occurs in philosophy through the fact that the “world is my world.”

The philosophical I is not the man, not the human body or the human soul of which psychology treats, but the metaphysical subject, the limit⁠—not a part of the world.

---

1. Rosser thought he had managed to condense PM into a single non-massive volume.

---

‡ . The axiom of reducibility is actually "a scheme, with one axiom for each superscript -- according to which any concept of any round is coextensive with one of the first round," writes John P. Burgess in Fixing Frege (Princeton 2005).

Since every formula determines a concept of some round or other, every formula in fact determines a concept of the first round, and we therefore have the following:

∃X⁰∀x(X⁰x <--> φ (x))

The subdivision of levels into types or "rounds" is in effect undone.

[Frank] Ramsey therefore proposed simply dropping the predicativity restrictions [rules against self-reference] and assuming unrestricted impredicative comprehension from the beginning [self-referencing permitted]. Russell had thought that his indirect procedure, of imposing predicativity restrictions and then undoing them by assuming reducibility, was somehow needed to block the semantic paradoxes like Grelling's heterological paradox. But Ramsey observed that these paradoxes depend on being able to express semantic notions, and that Russell's formalism provides no means of doing so.

The availability of the Wiener-Kuratowski definition of ordered pair [< a,b > = { a, {a,b} } ]  permitted another simplification of the system, namely, dropping all relational concepts. Thus one has in the end a simple hierarchy of one-place concepts – usually called "classes" – of levels one, two, three, and so on, in what is generally understood by "the theory of types" today.

Thomas Forster, in the Stanford Encyclopedia of Philosophy, gives an inkling of a form of type theory, NF, thus:

Some illustrations may help: x∈x is not stratified. x∈y is. Thus not every substitution-instance of a stratified formula is stratified. y=℘(x) is stratified (the fancy P means power set), with the variable y being given a type one higher than the type given to x. To check this we have to write out ‘y=℘(x)’ in primitive notation. (In primitive notation, this formula becomes: ∀z(z∈y <—> ∀w(w∈z —> w∈x)). One can assign 0 to w, 1 to z, and 2 to x, to get a stratification of this formula.) In general it is always necessary to write a formula out in primitive notation – at least until one gets the hang of it.

NF stands for "New Foundations for Mathematical Logic," a 1937 article by Willard Van Orman Quine proposing a simplified type theory. J. Barkley Rosser noted an inconsistency in the original NF, but he, Quine and others were able to repair it. In fact Rosser uses NF as a basis for part of his 1953 logic text. In 2017, M. Randall Holmes offered a proof that NF, as it now stands, is consistent [and incomplete].

Forster writes,

In the Theory of Types (as simplified successively by Ramsey, Carnap, Gödel and Quine) the bottom type is a collection of atoms. Atoms are non-sets (dormice, teapots, anything you please [aka ur-elements]) with no internal structure visible to the set theory. Thereafter type n+1 is simply the power set of type n, and there is a type for each natural number. The process cannot be extended to give transfinite types, since the types (being formally disjoint) are not cumulative so there is no sensible way to define a ω-th type.

In his 1937 paper Quine observed that "the theory of types has unnatural and inconvenient consequences. Because the theory allows a class to have members only of a uniform type, the universal class V gives way to an infinite series of quasi-universal classes, one for each type." [The American Mathematical Monthly Vol. 44, No. 2 (Feb., 1937), pp. 70-80 (11 pages).]

Similarly, the natural numbers cease to be unique, he said. For every type, one encounters, for example, a distinct 0.

His NF Theory was meant to remedy that defect.

I suppose we could use ~(x ∈ y●y ∈ x) as a set theory axiom. Substituting x for y, we then have ~(x e x) as a theorem. But, apparently such a fix is insufficient.

[No axiom is needed in the parallel case of ~(A ⊂ B ● B ⊂ A).

[A proper subset requires that A =/= B. If B is null, then so is A, but then A = B. So B may not be null if A is a proper subset. Hence A ∩ B =/= ∅ when A is a proper subset of B. Thus, the set of all squares of the naturals is a proper subset of N.

[The statement ~(A ⊂ B ● B ⊂ A)  is a theorem, not an axiom. That is, (A ⊂ B ● B ⊂ A) is false by x ∈ A --> x ∈ B ● x ∈ B --> x ∈ A, which defines equality.

[Just to be ultra-sure, we define a proper subset thus:
"u ∈ V --> u ∈ W ● u ∈ W -/-> u ∈ V"
So if we write x ∈ A --> x ∈ B ● y ∈ B --> y ∈ A,
on seeing that the letter x signifies any member of A, we are forced to conclude that y signifies at least one x, leading to the contradiction x_o ∈ A -/-> x_o ∈ B. ]